Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Hibbeler - Estática- Ed: 14º - Capítulo 10.Problemas - Ex. 79

Resolva o Problema 10.78 usando o círculo de Mohr.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

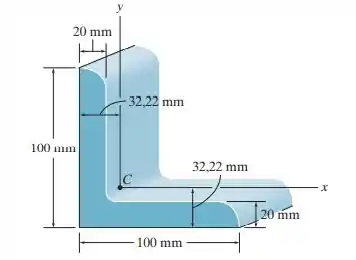
Primeiramente, vamos determinar os momentos de inércia em cada eixo:

I x = 1 12 20 100 3 + 10 0 20 50 - 32,22 2 + 1 12 8 0 2 0 3 + 8 0 2 0 32,22 - 10 2 = 3,142 × 10 6   m m 4

I y = 1 12 100 20 3 + 100 20 32,22 - 10 2 + 1 12 2 0 8 0 3 + 80 20 60 - 32,22 2 = 3,142 × 10 6   m m 4

Sabemos que:

I x y = ∑ I x ' y ' + A d x d y = - 32,22 - 10 50 - 32,22 100 20 - 60 - 32,22 × … … × ( 32,22 - 10 ) ( 80 ) ( 20 ) I x y = - 1,778 × 10 6   m m 4

Passo 2

Então, vamos contruir o círculo de Mohr. O centro do círculo é dado por:

O = I x + I y 2 = 3,142 × 10 6   m m 4

Logo, o raio do círculo vai ser:

R = I x - I y 2 + I x y 2 = 1,778 × 10 6   m m 4

Com isso, os momentos de inércia vão ser:

I m í n = 3,142 × 10 6 + 1,778 × 10 6   m m 4 = 4,92 × 10 6   m m 4 I m á x = 3,142 × 10 6 - 1,778 × 10 6   m m 4 = 1,36 × 10 6   m m 4

É isso, galera, Bora resolver mais questões pra ficar craque.

Resposta

I m í n = 4,92 × 10 6   m m 4 I m á x = 1,36 × 10 6   m m 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento de inércia polar em relação ao eixo z ' passando pelo centroide C da área é J C = 64210 6m m 4 . O momento de inércia em relação ao eixo y ' é 264 10 6 m m 4 , e o momento de inércia em rela
Determine o momento de inercia em relação ao eixo x .
Determine a localização y ¯ do centroide da área da seção transversal do canal e depois calcule o momento de inércia da área em relação a esse eixo.
Determine y ¯ , que localize o eixo centroidal x ’ da área da seção transversal da viga T , e depois determine os momentos de inércia I x ' e I y ' .
Determine o momento de inércia da área da seção transversal da viga em relação ao eixo y .