Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 7
Resolva o Problema 1.6 para as cargas internas resultantes que agem no ponto E.
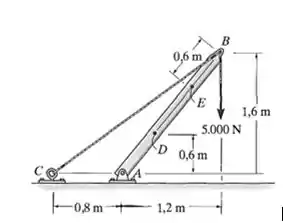
Passo 1
Primeiro, vamos fazero diagrama do corpo livre em relaçao ao segmento 
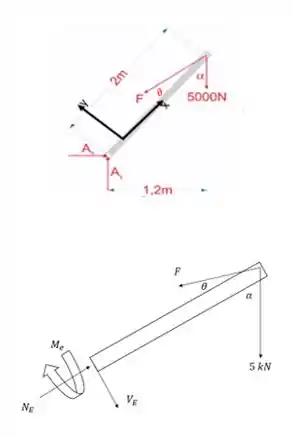
Passo 2
Para acharmos os ângulos e , basta olharmos para estes triângulos retângulos.
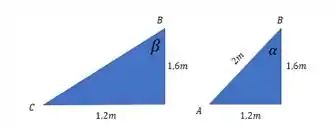
Passo 3
Primeiro, vamos usar o momento no ponto A.
Passo 4
Agora, para achar as cargas no ponto E, basta utilizar as equações de equilíbrio e do momento.
Resposta
Exercícios de Livros Relacionados
Represente graficamente os diagramas de força cortante e momento fletor para a viga. Ela é suportada por uma chapa lisa em A que desliza no interior de uma ranhura e, por isso não pode suportar uma fo
Faça os diagramas de força cortante e momento fletor para o eixo se ele for submetido às cargas verticais da correia, engrenagem e volante. Os mancais em A e B exercem somente reações verticais sobre
Determine o módulo da seção plástica e o fator de forma para a viga em I .
A coluna é construída de concreto de alta resistência e seis hastes de reforço de aço A-36. Se for submetida a uma força axial de 150 kN, determine o diâmetro exigido para cada haste, de modo que 1/4
Considere o problema geral de uma viga simplesmente apoiada submetida a n cargas concentras. Escreva um código computacional que possa ser usado para determinar a força cortante interna e o momento em