Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 186

Determine o módulo da seção plástica e o fator de forma para a viga em I .

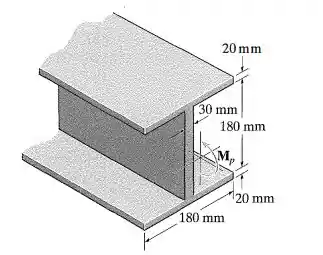
Passo 1

Primeiro, vamos fazer o DCL:

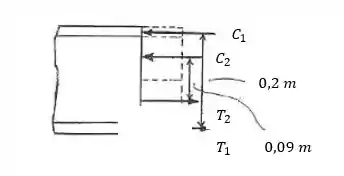
Passo 2

Agora, temos que aplicar a fórmula:

C 1 = T 1 = 0,18 × 0,022 × σ e = 3,6 × 10 - 3 σ e C 2 = T 2 = 0,060 × 0,03 × σ e = 2,7 × 10 - 3 σ e

M p = 2 0,1 C 1 + 0,45 C 2 = 9,63 × 10 - 4 σ e

Passo 3

Com isso, podemos calcular o momento de Inércia na viga:

I = 2 0,18 × 0,02 3 12 + 0,18 × 0,02 × 0,1 2 ) + ( 0,03 × 0,180 3 12 )

I = 8,682 × 10 - 5   m 4

Tendo o momento de inércia, vamos isolar o momento máximo:

σ e = M e C I

M e = 7,8927 × 10 - 4 σ e

Passo 4

Por fim, temos que o módulo da seção plástica é dado por:

k = M p M e

k = 9,63 × 10 - 4 σ e 7,892 7 × 10 - 4 σ e

k = 1,22

Já o fator de forma é dado por:

Z = M p σ e

Z = 9,63 × 10 - 4 σ e σ e

Z = 0,963 × 10 - 3

Resposta

k = 1,22

Z = 0,963 × 10 - 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Represente graficamente os diagramas de força cortante e momento fletor para a viga.
Represente graficamente os diagramas de força cortante e momento fletor para o eixo. Os mancais em A e B exercem somente reações verticais no eixo.
Represente graficamente os diagramas de força cortante momento fletor para o eixo. Os mancais em A e D exercem somente reações verticais sobre o eixo. A carga aplicada às polias em B, C e E
Um suporte de concreto armado é usado para apoiar as longarinas da plataforma de uma ponte. Represente graficamente os diagramas de força cortante e momento fletor para o suporte quando submetido à ca
Represente graficamente os diagramas de esforço cortante e momento fletor para o eixo. Os mancais em A e B exercem somente reações verticais sobre o eixo. Expresse também a força cortante e o momento