Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 40

Resolva o Problema 16.39 considerando que o disco A está inicialmente em repouso e que o disco B tem uma velocidade angular de 360 rpm no sentido horário.

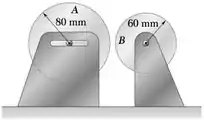
PROBLEMA 16.39 O disco A tem massa de 6 kg e velocidade angular inicial de 360 rpm no sentido horário; o disco B tem massa de 3 kg e está inicialmente em repouso. Os discos são ligados aplicando-se uma força horizontal de intensidade 20 N ao eixo do disco A. Sabendo que μ k = 0,15 entre os discos e desprezando o atrito no mancal, determine (a) a aceleração angular de cada disco, (b) a velocidade angular final de cada disco.

Passo 1

Enquanto ocorre o escorregamento, uma força de atrito F ↑ é aplicada ao disco A e F ↓ ao disco B.

Disco A:

I A = 1 2 m A r A 2 = 1 2 6   kg 0.08   m 2 = 0.0192   kg ∙ m 2

Σ F :             N = P = 20   N

F = μ N = 0.15 20 = 3   N

+ Σ M A = Σ M A eff :             F r A = I - A α A

3   N 0.08   m = 0.0192   kg ∙ m 2 α A

α A = 10.227

Passo 2

Disco B:

I - B = 1 2 m B r B 2 = 1 2 3   kg 0.06   m 2

= 0.0054   kg ∙ m 2

+ Σ M A = Σ M B eff :             F r B = I - B α B

3   N 0.06   m = 0.0054   kg ∙ m 2 α B

α B = 33.333   rad/ s 2

ω A 0 = 360   rpm 2 π 60 = 12 π   rad/s  

Passo 3

O deslizamento começa quando V C = V C ' . Isso é quando

ω A r A = ω B r B

α A t r A = ω B 0 - α B t r B

12.5   rad/ s 2 t 0.08   m = 12   π   rad/s - 33.333   rad/ s 2 t 0.06   m

t = 4.02124 ⇒ t = 0.75398   s

Passo 4

ω A = α A t = 12.5   rad/ s 2 0.75398   s = 9.4248   rad/s

+ ω A = 9.4248   rad/s 60 2 π = 90.00   rpm

+ ω B = ω B 0 - α B t

= 12 π   rad/s - 33.333   rad/ s 2 0.75398   s = 12.566   rad/s

ω B = 12.566   rad/s 60 2 π = 120.00   rpm

Resposta

α A = 12.50   rad/ s 2

α B = 33.3   rad/ s 2

ω A = 90.0   rpm  

ω B = 120.0   rpm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cursor A se desloca com velocidade constante v sobre a reta guia por um curto intervalo, enquanto o cursor B se desloca sobre a guia circular cujo centro está em O . Determine a velocidade angular ω
O ponto A recebe uma aceleração constante a para a direita a partir do repouso com x essencialmente nulo. Determine a velocidade angular ω da barra A B em termos de x e a .
28. . Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 50 ω 0,5r a d / s 2 , onde w é dado em rad/s. Determine a velocidade angular e o deslo
27. Por um certo período, a engrenagem A do motor de arranque do autmovel gira com uma aceleração angular a A = 450 t 2 + 60r a d / s 2 , onde t é dado em segundos. Determine a velocidade angular e o
39. Determine a velocidade e a aceleração da plataforma P como uma função do ângulo θ do came C se o came gira com uma velocidade angular constante ω . O pino de conexão não interfere no movimento de