Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 43

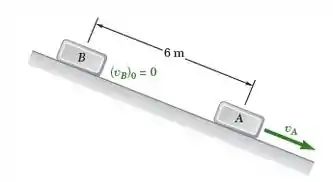
Caixas são colocadas em uma calha em intervalos uniformes de tempo t R e deslizam para baixo na calha com aceleração uniforme. Sabendo que quando uma caixa B qualquer é liberada, a caixa precedente A já deslizou 6 m , e que a 1 s depois elas estão a 10 m afastadas, determine (a) o valor de t R , (b) a aceleração das caixas.

Passo 1

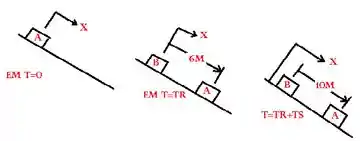
Deixei t s = 1 s seja o momento em que as caixas são 30 f t à parte.

Deixei a A = a B = a ;         ( x A ) 0 = ( x B ) 0 = 0 ;       ( v A ) 0 = ( v B ) 0 = 0 .

  1. Para t > 0 ,     x A = 1 2 a t 2

    2. Para t > t R ,   x B = 1 2 a   x   ( t - t R ) ²

    Em t = t R ,       x A = 18 f t           18 = 1 2 a t R 2

    Em t = t R + t S ,       x A - x B = 30 f t 30 = 1 2 a   x   t R + t S 2 - 1 2 a   x   t R + t S - t R 2 = 1 2 a t R 2 + a t R t S + 1 2 a t S 2 = 18 + a t R t S a t R = 30 - 18 t S = 12 1 = 12 f t / s

    Equação de divisão (1) de Eq. (2),

    1 2 a t R 2 a t R = 1 2 t R = 18 12

  2. Resolvendo Eq.(2) para a,

a = 12 3 = 4 f t / s ²

Resposta

  1. t R = 3,00 s
  2. a = 4,00 f t / s ²
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo de uma linha reta de maneira que a sua aceleração é a = 4 t 2 - 2m / s 2 , onde t é dado em segundos. Quando t = 0 , a partícula está localizada 2 m à esquerda da origem
Inicialmente, o carro move-se ao longo de uma estrada reta com uma velocidade de 35 m/s. Se os freios são aplicados e a velocidade do carro é reduzida a 10 m/s em 15 s, determine a desaceleração const
12.5. A posição da partícula é dada por s = 2 t 2 - 8 t + 6m , onde t é dado em segundos. Determine o tempo em que a velocidade da partícula é zero. Determine também a distancia total percorrida pela
Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 20 - 0,05 s 2 m / s , onde s é dado em metros. Determine a aceleração da partícula em s = 15m .
Uma partícula move-se ao longo de uma linha reta com uma velocidade de v = 4 t - 3 t 2 m s , onde t é dado em segundos. Determine a posição da partícula quando t = 4s . s = 0 quando t = 0 .