Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 18.Problemas - Ex. 39

Resolva o Problema 18.11 usando a equação de conservação de energia.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

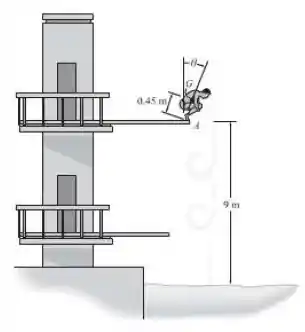
O problema 18.11 pede o número de revoluções que o homem completará antes de atingir a água.

Sabemos que sua massa é de 75   k g e que o raio de giração é dado por k G = 0,36   m .

Agora vamos aplicar conservação de energia:

T 1 + V 1 = T 2 + V 2

1 2 m 1 v 1 2 + m 1 g h 1 + 1 2 I G ω 1 2 = 1 2 m 2 v 2 2 + m 2 g h 2 + 1 2 I G ω 2 2

Sabemos que:

v A = 0,36 ω

v G = 0,45 ω

0 + 75 9,81 0,45 = 1 2 75 0,36 2 ω 2 + 1 2 75 0,45 ω 2

ω = 5,16   r a d / s

v G = 2,32   m / s

Passo 2

Podemos aplicar a velocidade encontrada na equação da posição do movimento acelerado, pois a aceleração da gravidade está agindo sob o movimento. Portanto, podemos encontrar o tempo de queda e associar com a posição θ no determinado momento. Temos que:

s = s 0 + v 0 t + 1 2 a t 2

9 = 0 + 2,32 t + 1 2 9,81 t 2

4,905 t 2 + 2,32 t - 9 = 0

t = 1,147   s

Logo:

θ = θ 0 + ω 0 t + 1 2 α t 2

θ = 0 + 5,16 1,147 + 0

θ = 5,92   r a d

Sabendo que 2 π equivale a uma volta, temos que:

θ = 0,942   r e v

Resposta

θ = 0,942   r e v

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra de 30k g é solta do repouso quando θ = 0 ° . Determine a velocidade angular da barra quando θ = 90 ° . A mola não está deformada quando θ = 0 ° .
A barra de 60k g , O A , é liberada do repouso quando θ = 0 ° . Determine sua velocidade angular quando θ = 45 ° . A mola permanece vertical durante o movimento e não está deformada quando θ = 0 ° .
A barra de 30k g é solta do repouso quando θ = 45 ° . Determine a velocidade angular da barra quando θ = 0 ° . A mola não está deformada quando θ = 45 ° .
A bola de 0,5 kg é disparada pelo dispositivo com mola mostrado. Determine a menor rigidez k necessária para disparar a bola e uma distância máxima s=750 mm plano acima após a mola ser empurrada para
No instante mostrado, o ponto P no cabo tem uma velocidade de v P = 12m / s , que está aumentando a uma taxa de a P = 6m / s 2 . Determine a potência de entrada do motor M neste instante se ele opera