Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas fundamentais - Ex. 12
No instante mostrado, o ponto P no cabo tem uma velocidade de , que está aumentando a uma taxa de . Determine a potência de entrada do motor M neste instante se ele opera com uma eficiência de . A massa do bloco A é 50 kg.
Passo 1
Começaremos o exercício encontrando as relações entre o deslocamento do sistema e o comprimento total do cabo:
Agora iremos encontrar o valor da aceleração do bloco A, sabendo que ela deve ser metade da aceleração do cabo, conforme mostrado na equação anterior. Sendo assim:
Passo 2
Agora iremos aplicar o somatório de forças na direção y para o bloco A conforme o diagrama a seguir:
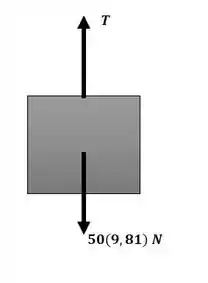
Passo 3
Agora iremos encontrar a potência de saída do motor:
E, dessa forma, a potência de entrada é dada por:
Resposta
Exercícios de Livros Relacionados
A bola de massa m é submetida a uma velocidade de v A = 5 g r na posição A. Quando ela chega a B , o cabo atinge o pino P, após o que a bola descreve uma trajetória circular menor. Se x = 2 3 r , dete
O anel liso de 10 kg é ligado à mola que tem um comprimento não estendido de 1,2 m. Se ele é solto do reposuso na posição A, determine a sua velocidade quando ele alcança o ponto B.
CB
O movimento da porta de garagem uniforme de 40 kg é guiado em suas extremidades pelo trilho. Determine a extensão inicial da mola requerida quando a porta é aberta, θ = 0°, de modo que, quando a porta
O movimento da porta de garagem uniforme de 40 kg é guiado em suas extremidades pelo trilho. Se a porta é liberada do repouso em θ = 0°, determine sua velocidade angular no instante θ = 30°. A mola es