Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 110

Resolva o Problema 2.109 supondo que os cabos foram substituídos por barras com a mesma área de seção transversal e o mesmo material. Supondo ainda que as barras foram fixadas de modo que possam suportar forças de compressão.

Passo 1

E ai pessoal tudo bem? Espero que sim !! o enunciado pede que a gente determine primeiramente a tensão máxima que ocorre no cabo BD. Antes vamos esboçar um diagrama de corpo livre, vem comigo :D

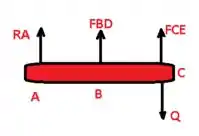
Sendo o θ = ângulo de rotação da barra rígida ABC temos a seguinte relação:

θ = δ B D L A B = δ C E L A c δ B D = L A B L A c δ C E = 1 2 δ C E

Considerando o equilíbrio da barra ABC, temos que fazer o somatório do momento em A :D

+ Σ M A = 0 :       L A B F B D + L A c F C E - L A c Q = 0 Q = F C E + L A B L A c F B D = F C E + 1 2 F B D

Agora vamos calcular a força em CE

F C E = A σ Y = 100   x   10 - 6   x   345   x   10 6 = 34,5   x   10 3 N (1)

Substituindo 1 aqui temos:

F B D = 2 Q - F C E = 2   x   50   x   10 3 - 34,5   x   10 3 = 31,0   x   10 3 N

Sendo F B D < A σ Y = 34,5   x   10 3 N , cabo BD é elástico quando Q = 50   k N

Passo 2

Partiu calcular a tensão, vem comigo :D

  1. Tensões máximas. σ C E = σ Y = 345   M P a σ B D = F B D A = 31,0   x   10 3 100   x   10 - 6 = 310   x   10 6 P a
  2. Máximo de deflexão do ponto C.

    3. δ B D = F B D L B D E A = 31,0   x   10 3   x   ( 2 ) 200   x   10 9   x   ( 100   x   10 - 6 )   = 3,1   x   10 - 3 m

    Substituindo (1) aqui temos:

    δ C = δ C E = 2 δ B D = 6,2   x   10 - 3 m

    Descarregando. Q ' = 50   x   10 3 N ,       δ ' C E = δ ' C

    De (1), δ ' B D = 1 2 δ ' C

    Considerando as seguintes forças temos:

    F * B D = E A δ ' B D L B D = 200   x   10 9     x     100   x   10 - 6     x   ( 1 2 δ ' C ) 2 = 5   x   10 6 δ ' C  

    F ' C E = E A δ ' C E L C E = 200   x   10 9     x     100   x   10 - 6     x   ( δ ' C ) 2 = 10   x   10 6 δ ' C Q = F ' C E + 1 2 F ' B D = 12,5   x   10 6 δ ' C  

    Equação de expressão para Q ' , 12,5   x   10 6 δ ' C = 50   x   10 3 δ ' C = 4   x   10 - 3 m

  3. Deslocamento final.

δ C = ( δ C ) m - δ ' C = 6,2   x   10 - 3 - 4   x   10 - 3 = 2,2   x   10 - 3 m  

Resposta

  1. σ B D = 310   M P a
  2. 6,20   m m   ↓
  3. 2,20   m m   ↓
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a ponte em treliça Pratt e o carregamento mostrado, determine a tensão normal média no elemento BE, sabendo que a área da seção transversal desse membro é 5,87 in².
A conexão AC tem seção transversal retangular uniforme 1/8 in de espessura e 1 in de altura. Determine a tensão normal na porção central da conexão.
Uma barra de reboque para aviões é posicionada utilizando um cilindro hidráulico conectado por uma haste de aço com diâmetro de 25 mm a dois dispositivos de braços e rodas DEF. A massa de toda a barra
A conexão BD consiste em uma barra simples de 1 in. de altura por 1/2 in. de espessura. Sabendo que cada pino possui tem diâmetro de 3/8 in determine o valor máximo da tensão normal média na conexão B
Três forças, cada uma de intensidade P= 4 kN, são aplicadas a estrutura mostrada. Determine a área da seção transversal da parte uniforme da haste BE para a qual a tensão normal é de +100 MPa.