Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 51

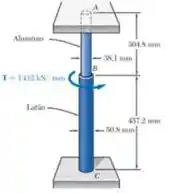
Os cilindros de seção transversal cheia AB e BC estão conectados em B e engastados em suportes fixos de A e em C. Sabendo os módulos de rigidez são 25.5 GPa para o alumínio e 38.6 GPa para o latão, determine a máxima tensão de cisalhamento (a) no cilindro AB e (b) no cilindro BC.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a máxima tensão de cisalhamento) no cilindro AB e no cilindro BC.

No cilindro AB temos os seguintes dados:

G = 25,5   G P a  

c = 1 2 d = 1 2 38,1 = 19,05   m m

c = 0.01905   m

L =   304,8   m m

L = 0.3048   m

Calculando J temos:

J = π 2 c 4 = π 2 0.01905 4 = 206.87 × 10 - 9 m 4

φ B = T A B L G J = T A B ( 0.3048 ) 25.5 × 10 9 206.81 × 10 - 9  

= 57.797 × 10 - 6   T A B

Passo 2

No cilindro BC temos os seguintes dados

G = 38,6   G P a  

c = 1 2 d = 1 2 50,8 = 25,4   m m

c = 0.0254   m

L =   457,2   m m

L = 0.4572   m Calculando J temos:

J = π 2 c 4 = π 2 0.0254 4 = 653.81 × 10 - 9   m 4

φ B = T B C L G J = T B C ( 0.4572 ) 38.6 × 10 9 653.81 × 10 - 9  

18.12 × 10 - 6   T B C

Passo 3

Expressões correspondentes para ϕ B temos:

57.797 × 10 - 6   T A B = 18.12 × 10 - 6   T B C

T B C = 3,1897   T A B

Equilíbrio de ligação em B :

T A B + T B C - T = 0

T = 1412   k N ⋅ m m   =   1,412 × 10 3 N ⋅ m m

T A B + T B C = 1.412 × 10 3

4,1897   T A B = 1.412 × 10 3

Calculando os torques de todas as sessões temos:

T A B = 1.412 × 10 3 4.1897 = 337.02   N ⋅ m

T B C = 3,1897   T A B

T B C = 337.02 × 3,1897 = 1.075   k N ⋅ m

Passo 4

  1. Máxima Tensão no cilindro AB

    2. T A B = T A B c J = 337.02 0.01905 206.87 × 10 - 9

    T A B = 31.035   M P a

  2. Máxima Tensão no cilindro BC

T B C = T B C c J = 1.075 × 10 3 0.0254 653.81 × 10 - 9

T B C = 41.76   M P a

Resposta

(a)   31,035   M P a

(b) 41,76   M P a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O navio em A está começando a perfurar um poço de petróleo no fundo do oceano a uma profundidade de 1524 m. Sabendo que o topo da broca de aço G = 77,2G P a de 203 mm de diâmetro dá duas voltas comple
O eixo cheio AB tem diâmetro d s = 1.5i n , e é feito de aço com G = 11,2X 10 6 psi e τ a l l = 7 psi, enquanto a luva CD é feita de latão com G=5,6 x 10 6 psi e τ a l l = 7 ksi. Determine o maior âng
Três eixos se seção transversal cheia são conectados pelas engrenagens A e B mostradas. Sabendo que G = 77,2 GPa, determine o ângulo de torção entre (a) A e B (b) A e C.
(a) Para o eixo de alumínio mostrado G = 27G P a , determine o torque T 0 que provoca um ângulo de torção de 2° e (b) o ângulo de torção provocado pelo mesmo torque T 0 em um eixo cilíndrico cheio de
A barra de alumínio A B G = 27G P a está ligada a barra de latão B D G = 39G P a . Sabendo que a parte CD da barra de latão é vazada e tem um diâmetro interno de 40 mm, determine o ângulo de torção em