Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 116

Sabendo-se que a tensão admissível na seção ABD é 70 MPa, determinar a maior força P que pode ser aplicada ao suporte mostrado.

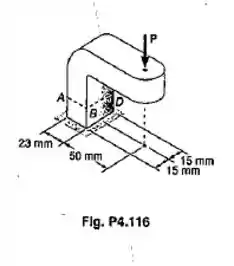
Passo 1

Do enunciado nós já temos que

σ m a x = 70   M P a

Com uma força aplicada ali naquele ponto P que o enunciado se refere, teremos para o somatório dos momentos

M = p × 0,0615

E o momento inpercia fica

I = b h 3 12 = 0,03 × 0,023 3 12 = 3,042 × 10 - 8   m 4

Teremos ainda que a área da seção cortada é

A = 0,023 × 0,03 = 6,9 × 10 - 4   m 4

Passo 2

Para o σ 0 teremos

σ 0 = - P A = - P 6,9 × 10 - 4

Lembrando que esse P é justamente o que queremos.

Passo 3

Para encontrarmos o valor de P precisamos lembrar que

σ m a x = σ 0 + M c I → 70 × 10 6 = - P 6,9 × 10 - 4 + P × 0,0615 × 0,0115 3,042 × 10 - 8

Isolando o P encontramos

70 × 10 6 = 23,25 × 10 3 × P + 1,449 × 10 3 × P

P = 70 × 10 6 21,801 × 10 3

P = 3211   N

Resposta

P = 3,211   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga de seção transversal assimétrica está submetida a um momento M 0 atuando no plano vertical x y . Mostre que a tensão no ponto A, de coordenadas y e z , é σ A = - y I y - z I y z I y I z - I y
A barra curva mostrada tem seção transversal de 40 x 60 mm e raio interno r 1 = 15m m . Para o carregamento mostrado, determine as maiores tensões de tração e compressão.
Resolva o Problema 4.167 considerando que β = 60 ° .
As chapas de ligação de aço com a seção transversal mostrada na figura estão disponíveis com diferentes ângulos centrais β . Sabendo que a tensão admissível é de 82,7 MPa, determine a maior força P qu
Para a barra curva e o carregamento mostrado, determine o erro percentual introduzido na computação da tensão máxima admitindo que a barra é reta. Considere o caso em que (a) r 1 = 20m m , (b) r 1 = 2