Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 49
Resolva o Problema 7.27 usando o círculo de Mohr.
Passo 1
Beleza! Esse exercício vai ser resolvido somente com o auxílio da equação para o raio do círculo de Mohr e vamos lembrar um pouquinho do ensino médio também :).
Passo 2
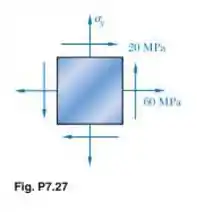
Então vamos lá! Vamos começar escrevendo as tensões que temos de acordo com o elemento dado no enunciado, então teremos:
Então, se o enunciado nos disse que a tensão de cisalhamento máxima no plano das tensões tem que ser igual ou menor que 75 MPa, vamos tomar o caso limite, em 75 MPa. Sabemos que esse valor de cisalhamento corresponde ao raio do círculo de Mohr, então teremos:
Passo 3
Agora então, sabendo que a equação para o raio do círculo de Mohr é dada por:
Podemos isolar dessa equação, já que temos todos os outros valores e queremos justamente o valor de , então, fazendo isso, teremos:
Substituindo os valores conhecidos nessa equação, chegamos em uma equação do 2º grau para , onde teremos:
Isso mesmo que você está pensando, vamos ter que aplicar Bháskara para resolver essa equação. Relembrando a fórmula de Bháskara, temos:
Então, para o nosso caso, teremos:
Esses dois valores estão dentro do limite máximo de 75 MPa para o cisalhamento, mas como o enunciado nos pediu o maior valor, em módulo, nossa resposta será: