Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 60
60. Resolva o Problema 9.6 usando o círculo de Mohr.
Passo 1
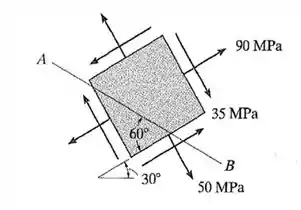
Da seguinte figura de estado plano, tiramos que:
Passo 2
Como estamos trabalhando com Círculo de Mohr, a primeira coisa a se fazer é determinar o centro do círculo, que é dado por:
Substituindo os valores numéricos correspondentes, chega-se à:
E em seguida, vamos determinar o raio do nosso círculo, através da fórmula da tensão de cisalhamento máximo:
Trocamos as variáveis pelos seus respectivos valores numéricos
Passo 3
Agora, voltemos até a figura do enunciado. O nosso elemento faz um ângulo de com a horizontal. Mas esse valor não nos interessa. Queremos o valor do ângulo com a vertical e seu sentido. Ora bolas, esse ângulo é nada mais nada menos que o complemento de , ou seja, . Para construir o círculo, como trabalhamos com o dobro do ângulo em questão, logo iremos realizar tudo tomando como ponto de partida um ângulo de .
Visto que já achamos a posição do centro do nosso círculo e o raio dele, vamos construí-lo em um esboço. Lembre-se bem que como a tensão cisalhante é negativa, considereraremos a parte de cima do círculo em nossa construção:
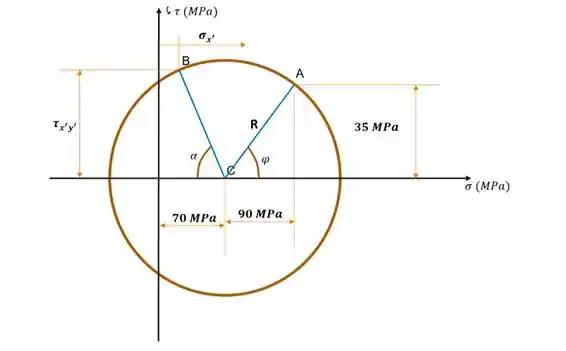
Para calcular nossas tensões e precisamos do ângulo . Se você reparar bem na figura acima, esse ângulo é dado por:
O ângulo , bem, é o replemento daquele ângulo lá, de . Ou seja, . Agora, o ângulo , se você reparar naquele da figura (onde está a tensão de , nós podemos obter como:
Então, obtemos o valor de como sendo o resultado da operação abaixo:
Voltemos ao que interessa! Ao analisar o círculo, por relação trigonométrica, tiramos que:
E como temos os valores:
Susbstituímos nas duas fórmulas anteriores das tensões:
Alcançamos nosso resultado: