Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 64
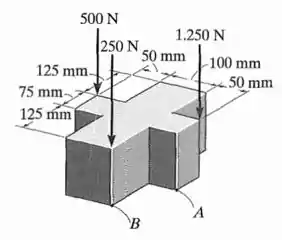
O bloco está sujeito às três cargas axiais mostradas na figura. Determine a tensão normal desenvolvida nos pontos A e B. Despreze o peso do bloco.
Passo 1
Fala galerinha bonita, tudo beleza?!
Nesse exercício aqui queremos as tensões normais em e , portanto temos que levar em conta o fator das forças axiais e da flexão.
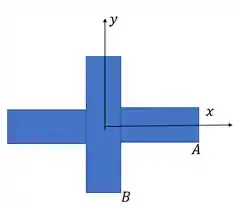
Vamos começar achando os esforços normais. Vamos considerar como eixo o eixo paralelo ao segmento de 75 mm. Calculando o momento temos:
E para :
E por somatório de forças temos a força total no eixo :
E vamos aproveitar para calcular a área:
Belezoca, agora que tiramos essas informações importantíssimas, bora lá ver como fica essa brincadeira!
Passo 2
Calculamos agora os momentos de inércia em ambos os eixos e , então para o eixo vamos obter que:
E para o eixo , obtemos que:
Passo 3
Calculamos então as tensões em ambos os pontos. Todos sofrem compressão por causa das forças. Precisamos ver os sinais das tensões causadas pelos momentos:
Para achar onde é tração ou compressão, você coloca seu dedão da mão direita na direção do vetor momento. Ao girar a mão, a região de compressão é onde seus dedos entram no plano da folha.
Em , causa tração (positivo) e em causa compressão (negativo).
Para fazemos pensamento parecido:
Onde e são as distâncias dos pontos A ou B até os eixos centrais X ou Y.