Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 65
Se P = 15 kN, desenhe o gráfico da distribuição de tensão que age na seção transversal a-a do elo fora de centro.
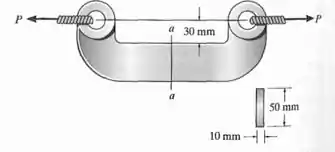
Passo 1
Faremos somatório de força e momento para obtermos as forças atuando na seção
Diagrama do corpo livre na seção a-a
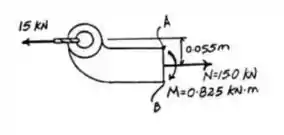
Passo 2
Agora calculamos as tensões. Podemos perceber pela direção do momento que teremos compressão em baixo e tração em cima.
Onde C é igual a distância da borda até o centro da seção transversal
Passo 3
Fazer o Gráfico
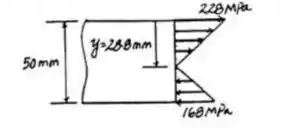
Podemos obter o Y por simples regra de 3
Resposta
Gráfico acima.
Exercícios de Livros Relacionados
O painel de sinalização está sujeito à carga uniforme do vento. Determine as componentes da tensão nos pontos A e B no poste de sustentação de 100 mm de diâmetro. Mostre os resultados em um elemento d
O painel de sinalização uniforme pesa 7,5 kN e é suportado pelo tubo AB que tem raio interno de 68 mm e raio externo de 75 mm. Se a parte frontal do painel estiver sujeita a uma pressão uniforme do ve
A haste maciça está sujeita à carga mostrada na figura. Determine o estado de tensão desenvolvido no material no ponto C e mostre os resultados em um elemento de volume diferencial nesse ponto.
A lança de guindaste é submetida a uma carga de 2,5 kN. Determine o estado de tensão nos pontos A e B. Mostre os resultados em um elemento de volume diferencial localizado em cada um desses pontos.
A haste maciça de 25 mm de diâmetro está sujeita às cargas mostradas na figura. Determine o estado de tensão no ponto B e mostre os resultados em um elemento diferencial localizado nesse ponto