Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 17
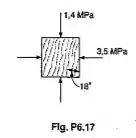
As fibras de uma peça de madeira formam um ângulo de 18 graus com a vertical. Para o estado de tensões mostrado determinar: (a) a tensão de cisalhamento no plano, em um plano paralelo as fibras;(b) a tensão normal perpendicular as fibras
Passo 1
E aí, prontinho pra mais um exercício?
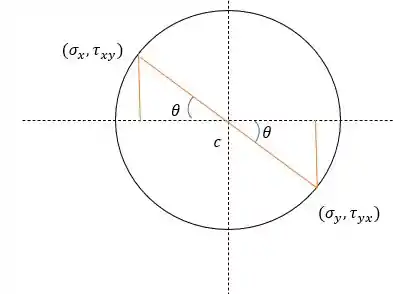
Mais uma de círculo de Mohr, e se liga aqui! Já que não temos tensão cisalhante foi nos dado o ponto das tensões principais.
E aquela ideia, se giramos 18 graus o elemento no sentido anti-horário, vamos girar 36 graus no sentido horário.
Passo 2
Agora é de boas, nossa referência é o sigma x, então bora calcular as tensões no novo ponto. Lembrando que tem que ser a partir do eixo x no primeiro quadrante, sendo assim:
Assim o item a.
Passo 3
E para o item b, vamos calcular a tensão normal que pode ser dada por:
Resposta
(a)
(b)