Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 50

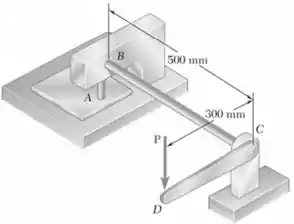
Um furo é feito em uma chama de plástico em A através de uma força P de 600 N, aplicada a uma extremidade D da alavanca CD, que está rigidamente conectada ao eixo cilíndrico BC . Especificações do projeto exigem que o deslocamento do ponto D não exceda 15 mm desde o momento em que o punção toca a chapa até o ponto em que ele efetivamente penetra o plástico. Determine o diâmetro necessário para o eixo BC feito com aço G - 77,2   G P a e τ a d m = 80   M P a .

Passo 1

E ai gurizada tudo belezinha? Para determinarmos o diâmetro necessário para o eixo BC. Comecemos calculando pelo torque:

T = r P = 0.300   m 600   N = 180   N / m

Agora gurizada, vamos para o diâmetro do eixo, mas usando como base o limite de deslocamento:

φ = δ r = 15   m m 300   m m   = 0.005   r a d φ = T L G J = 2 T L π G c 4

c 4 = 2 T L π G φ = 2 180 0.500 π 77.2 × 10 9 0.05 = 14.483 × 10 - 9   m 4

c = 11.038 × 10 - 3   m = 11.038   m m d = 2 c = 22.1   m m

E agora, vamos ver o diâmetro do eixo, mas com base na tensão:

τ = 80 × 10 6   P a τ = T c j = 2 T π c 3

c 3 = 2 T π τ = 2 180 π 80 × 10 6 = 1.43239 × 10 - 6   m 3

c = 11.273 × 10 - 3 m = 11.273   m m d = 2 c = 22.5   m m

d = 22.5   m m

Resposta

Então gurizada, o diâmetro do eixo, usando o maior valor para atender a todos os limites, é: d = 22.5   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As extremidades A e D dois eixos sólidos AB e CD são fixas, enquanto as extremidade B e C são conectadas por engrenagens conforme mostrado. Sabendo que a tensão de cisalhamento admissível é de 50 MPa
A barra de alumínio B C G = 26G P a está ligada a barra de latão A B G = 39G P a . Sabendo que cada barra é seção cheia e tem um diâmetro de 12 mm, determine o ângulo de torção (a) em B (b) em C
Determine o maior diâmetro possível para a barra de aço com 3,0 m de comprimento G = 77,2G P a , se a barra deve ser girada em 30° sem exceder a tensão de cisalhamento de 80 MPa.
500 N ⋅ m no eixo de alumínio ABCD, quando ele está girando a uma rotação constante. Sabendo que G = 27 GPa e que os torque exercidos sobre as polias B e C são aquelas mostrados na figura, determine o
O eixo cheio AB tem um diâmetro d s = 1.75i n e é feita de aço com G = 11.2 × 10 6 p s i e τ a l l = 12K s i , enquanto a luva CD é feita de latão com G = 5.6 × 10 6 p s i e τ a l l = 7K s i . Determi