Resolver o Prob. 5.120, considerando que a espessura da placa é de e é dobrada para formar o perfil mostrado.
Passo 1
Temos a seguinte situação:
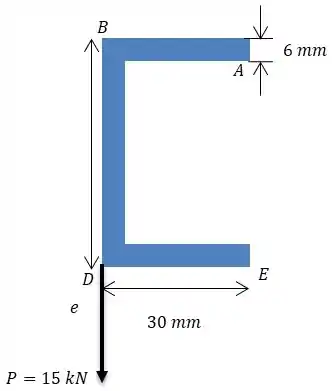
Temos que determinar o torque que irá torcer esta seção na letra (a), para isto vamos precisar determinar a tensão de cisalhamento e o centro de cisalhamento.
Temos uma boa notícia, temos um exemplo feito no livro com uma viga de mesmo perfil de viga. Exemplo 5.4, página 561.
Passo 2
a)Neste exemplo(5.4) ele determinar uma equação para o centro de cisalhamento, que resulta em:
Aqui temos: , e .
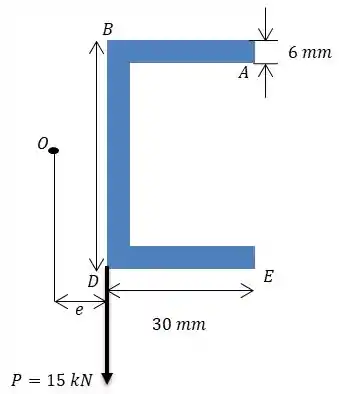
Calculando o centro de cisalhamento:
Multiplicando por para unidade ficar em metros:
Passo 3
a) Por definição nossa força de cisalhamento é o próprio :
E finalmente podemos calcular o torque:
Passo 4
b)A tensão de cisalhamento máxima é devido ao efeito conjunto da flexão e da torção que ocorre na linha neutra, na face da alma.
Temos que a tensão máxima será a soma das duas:
E a tensão de cisalhamento de torção.
Vamos começar pela tensão de cisalhamento de flexão. Temos , .
Temos que calcular o momento de inércia e o momento estático.
Calculando o momento de inércia, temos o momento de inércia da alma (retângulo vertical) e 2 momentos de inércia das abas (retângulos horizontais):
Temos , e . Substituindo estes valores:
Multiplicando por para unidade ir para metros:
Passo 5
Partindo para o cálculo do momento estático:
Calcularemos o momento estático da parte superior da seção transversal em relação à linha neutra:
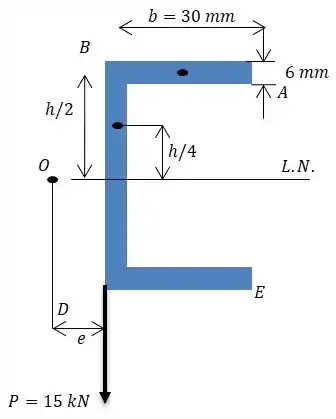
Para aba:
Para alma:
Executando o momento estático:
Substituindo valores:
Convertendo para metros, multiplicando por :
Passo 6
Temos todas variáveis para determinar a tensão de cisalhamento por flexão:
Substituindo todas as unidades:
Lembrando que em metros será .
Passo 7
Para determinar a tensão de cisalhamento por torque ou torção, temos:
Temos , calculado na letra (a),
Temos que determinar e :
O termo é o somatório de todo o comprimento da viga, logo:
Convertendo para metros:
E possui uma fórmula definida por:
Substituindo todos os valores:
Como temos todas variáveis para determinar , basta substituir todas as variáveis:
Passo 8
Finalmente teremos a tensão cisalhante máxima:
Resposta
a)
b)