Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 118

Determinar a localização do centro de cisalhamento O da viga de parede fina com espessura uniforme, da seção transversal mostrada.

Passo 1

Nosso objetivo é determinar a localização do centro de cisalhamento O da viga de parede fina.

Para calcular isto, vamos integrar o fluxo de cisalhamento sobre a viga para determinar a forças internas. Após isto, vamos fazer o cálculo do momento equivalente para determinar distância e .

Passo 2

Começando com o cálculo do momento de inércia.

Possuímos 3 retângulos e não consideremos o momento de inércia da viga central. Pois, o momento de inércia deste retângulo com relação ao eixo é muito pequeno para ser considerado.

Por definição temos o momento de inércia:

I = 1 12 t h 1 3 + 1 12 t h 2 3 + 1 12 + t h 3 3

Passo 3

Vamos determinar a força na aba esquerda.

F 1 = ∫ τ d A

Em que a tensão cisalhante média é:

τ = V Q I t

Temos que determinar nosso momento estático para dar continuidade, sobre a força cisalhante fique tranquilo que ira ser simplificada.

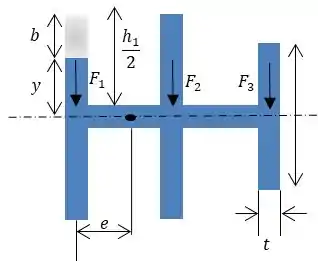
Determinando o momento estático:

Q = A ∙ y ¯

Precisamos determinar a área da aba:

A = b ∙ t

A = 1 2 h 1 - y ∙ t

Determinando o centroide da nossa aba:

y ¯ = 1 2 h 1 + y ∙ 1 2

Efetuando a multiplicação:

Q = 1 2 h 1 - y 1 2 h 1 + y ∙ 1 2 ∙ t

Q = 1 4 h 1 2 - y 2 1 2 ∙ t

Passo 4

Agora que temos o momento de inércia estático, podemos determinar F 1 :

Para determinar F 1 , vamos deixar claro nossa tensão cisalhante.

τ = V Q I t

Substituindo o momento estático:

τ = V I t 1 4 h 1 2 - y 2 1 2 ∙ t

Temos que F 1 é definido por:

F 1 = ∫ τ d A

F 1 = ∫ V I t 1 4 h 1 2 - y 2 1 2 ∙ t d A

Simplificando t e inserindo os limites de integração para a variável d y

d A d y = 1 2 h 1 - y ∙ t

d A = 1 2 h 1 - y ∙ t d y  

d A = - t   d y

Vamos considerar o meio da viga h 1 2 como coordenada zero, logo, teremos F 1 indo de - h 1 2 até + h 1 2

Substituindo na integral:

F 1 = ∫ - h 1 / 2 h 1 2 - t V I 1 4 h 1 2 - y 2 1 2   d y

F 1 = - V t 1 2 I ∙ 1 4 h 1 2 y - y 4 3 - h 1 2 h 1 2

Aplicando os limites de integração:

F 1 = - V t 2 I ∙ 1 4 h 1 2 ∙ h 1 2 - h 1 2 3 3     + 1 4 h 1 2 ∙ h 1 2 + - h 1 2 3 3    

F 1 = - V t 2 I ∙ h 1 3 8 - h 1 3 24     + h 1 3 8 - h 1 3 24      

F 1 = - V t 2 I ∙ 2 h 1 3 24     + 2 h 1 3 24      

F 1 = - V t 2 I ∙ 4 h 1 3 24

F 1 = - V t I ∙ h 1 3 12

Por final, vamos substituir o momento de inércia:

F 1 = - V t ∙ h 1 3 t h 1 3 + t h 2 3 + t h 3 3

Passo 5

Agora temos uma notícia boa, este detalhe do enunciado, “parede fina com espessura uniforme”, todas as forças F 1 , F 2 e F 3 terão o mesmo cálculo.

Unicamente oque ira diferenciar é a coluna

F 2 = - V t ∙ h 2 3 t h 1 3 + t h 2 3 + t h 3 3

F 3 = - V t ∙ h 3 3 t h 1 3 + t h 2 3 + t h 3 3

Claro, caso você desejar executar os cálculos novamente e verificar, eles devem resultar nisso.

Passo 6

Como temos todas as forças atuantes, podemos executar o cálculo do momento equivalente para determinara distância e .

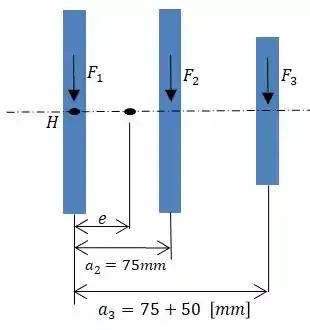
Considerando sentido anti-horário positivo.

∑ M H = 0

V e + F 1 ∙ 0 + F 2 ∙ a 2 + F 3 ∙ a 3 = 0

V e + - V t ∙ h 2 3 t h 1 3 + t h 2 3 + t h 3 3 ∙ a 2 + - V t ∙ h 3 3 t h 1 3 + t h 2 3 + t h 3 3 ∙ a 3 = 0

Isolando e :

V ∙ e = V t ∙ h 2 3 t h 1 3 + t h 2 3 + t h 3 3 ∙ a 2 + V t ∙ h 3 3 t h 1 3 + t h 2 3 + t h 3 3 ∙ a 3

Simplificando V e t :

e = h 2 3 h 1 3 + h 2 3 + h 3 3 ∙ a 2 + h 3 3 h 1 3 + h 2 3 + h 3 3 ∙ a 3

Substituindo h 1 = h 2 = 125   m m e h 3 = 100   m m

e = 125 3 125 3 + 125 3 + 100 3 ∙ 75 + 100 3 125 3 + 125 3 + 100 3 ∙ 75 + 50

e = 55   , 334   m m

Resposta

e = 55   , 334   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O projeto de uma viga requer a soldagem de quatro placas horizontais à uma placa vertical de 12,7x127 mm como mostrado. Para uma força cortante vertical V determinar a dimensão h para que o fluxo de c
Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi
Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi
Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensã
A seção transversal de uma viga extrudada é uma seção quadrada vazada de lado a = 75m m e espessura t = 6,35m m . Para uma força cortante vertical 65k N , determinar a máxima tensão de cisalhamento na