Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 127
A viga em balanço consiste de perfil “U” de espessura uniforme. Sabendo-se que a carga atua no centro de cisalhamento e no plano da seção de extremidade da viga, determinar a tensão de cisalhamento no: ponto ; ponto .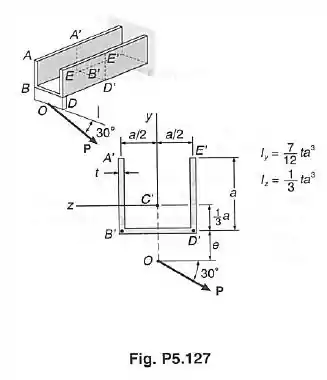 
Passo 1
a)Para determinar atenção de cisalhamento no ponto , temos que determinar o momento de inércia, o momento estático e tensão que passa por este ponto todos eles em função de .
Como própria imagem do exercício nos mostra, temos o momento de inércia por e . Como nosso vetor será composto por estas coordenadas, determinaremos a tensão cisalhante por e por .
Assumiremos que a vigar não sofrera torção, logo, apenas teremos tensão de cisalhamento por flexão.
Passo 2
Vamos decompor nosso vetor , como ele está com uma inclição de com a horizontal, decompondo nas coordenadas ,para horizontal, e ,para vertical, temos o seguinte triângulo retângulo.
Aplicando trigonometria, temos:
Para outra componente:
Passo 3
Falta determinar o momento estático:
Em que , será a área de seção do nosso ponto:
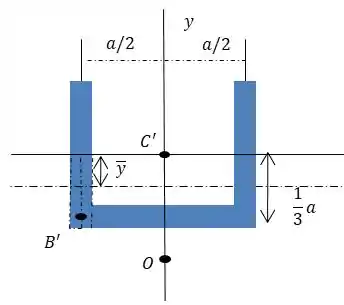
E , é a distância do centro da nossa área hachurada até . Como mostra na figura ela será
Teremos o momento estático como:
Passo 4
Como temos todas as informações necessária, basta substituir na fórmula da tensão por cisalhamento que é definida por:
Passo 5
Determinando para coordenada :
Passo 6
A tensão de cisalhamento total no ponto :
Passo 7
b) Para ponto a tensão será equivalente a . Pois, nossa figura é simétrica.
Resposta
a)
b)