Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 54a

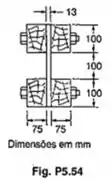
Uma viga composta é feita de madeira e duas chapas de aço, unidas com parafusos, como mostrado. Sabendo-se que os parafusos são de 16   m m de diâmetro e espaçados longitudinalmente de 200   m m , os módulos de elasticidade valem 200   G P a e 13   G P a , para o aço e para a madeira, repectivamente, e está sujeita a uma força cortante vertical de 17,8   k N , determinar (a) a tensão de cisalhamento média nos parafusos (b) a tensão de cisalhamento no centro da seção transversal. (Sugestão: Usar o método indicado no prob. 5.52)

Passo 1

Pra começar, vamos transformar a região de madeira para uma região metálica.

n = E m a d e i r a E a ç o = 13 200 = 0.065

Assim, podemos multiplicar a espessura da madeira, e substituir por uma região de aço:

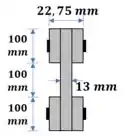
Passo 2

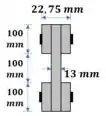
Agora vamos calcular o momento de inércia da seção transformada:

I = 22,75 ⋅ 300 3 12 - 22,75 ⋅ 100 3 12 + 13 ⋅ 100 3 12

I = 50,38 ⋅ 10 6   m m 4

Passo 3

Beleza!

Pra calcular a tensão no parafuso, primeiro a gente precisa do momento estático no ponto onde as placas se conectam:

Q = 4,875 ⋅ 100 ⋅ 100 = 48750   m m 3

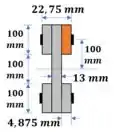
Logo, o fluxo de cisalhamento no parafuso é:

q = V Q I = 17800   N ⋅ 48750   m m 3 50,38 ⋅ 10 6   m m 4 = 17,2 4 N m m

Passo 4

A questão está praticamente resolvida.

Como a gente já tem o fluxo de cisalhamento, podemos calcular a força sobre o parafuso. Lembre-se que o espaçamento entre parafuso é s = 200   m m

F p = q ⋅ s = 86,74 N m m ⋅ 200   m m = 3,45   k N

A área transversal dos parafusos é:

A = π d 2 4 = π ⋅ 16 2 4 = 201,06   m m 2

E com isso a gente calcula a tensão sobre os parafusos:

τ p = F p A = 3450   N 201,06   m m 2 = 17,14   M P a

Resposta

τ p = 17,14   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos D e E : (a) a maior tensão normal.
146. A viga caixão é mostrada é feita de quatro pranchas firmemente coladas. Sabendo-se que na junta colada a tensão admissível de cisalhamento é de 830k P a , determinar: (a) a maior força cortante v
147. Para a viga caixão do problema 5.146 , determinar (a) a maior força cortante horizontal permissível na viga; (b) a correspondente tensão de cisalhamento máximo na viga
148. Duas forças são aplicadas a um tubo A B , como mostrado. Sabendo-se que o tubo tem diâmetros, interno e externo, iguais a 35m m e 42m m , respectivamente, determinar as tensões, normal e de cisal
149. Resolver o problema 5.148 , considerando que a força de 1500N é dirigida para cima