Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 127

O torque T causa uma rotação de 0,6° na extremidade B da barra de alumínio mostrada, Sabendo que b = 15   m m   e   q u e   G = 26   G P a , determine a máxima tensão de cisalhamento na barra.

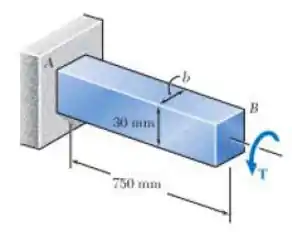
Passo 1

E ai gurizada tudo beleza? O enunciado pede que a gente determine a máxima tensão de cisalhamento na barra. Então vamos trazer os dados ;D

a = 30   m m = 0,030   m b = 15   m m = 0,015   m φ = 0,6 ° = 10,472   x   10 - 3 r a d

Passo 2

A relação a/b é dada a partir de;

φ = T L c 2 a b 3 G         ∴         T = c 2 a b 3 G φ c 1 L τ m a x = T c 1 a b 2 = c 2 a b 3 G φ c 1 a b 2 L = c 2 b G φ c 1 L a b = 30 15 = 2,0

Da tabela 3.1,

c 1 = 0,246 c 2 = 0,229

Agora sim podemos determinar a tensão de cisalhamento :D

τ m a x = 0,229   x   15   x   10 - 3   x   26   x   10 9   x   10,472   x   10 - 3 0,246   x   750   x   10 - 3 = 5,07   x   10 6 P a

Resposta

τ m a x = 5,07   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra de alumínio A B G = 27G P a está ligada a barra de latão B D G = 39G P a . Sabendo que a parte CD da barra de latão é vazada e tem um diâmetro interno de 40 mm, determine o ângulo de torção em
No Problema 3.114, determine o ângulo de torção permanente da barra.
Dois eixos de seção transversal cheia, cada um com 30 mm de diâmetro, são conectados pelas engrenagens mostradas. Sabendo que G=77,2 GPa, determine o ângulo que extremidade em A descreve quando um tor
Uma barra de aço é usinada até a forma mostrada na figura, para obter um eixo cônico de seção transversal cheia ao qual são aplicados torque de intensidade T = 8473k N ⋅ m m . Considerado que o aço se
Se torques aplicados ao eixo cônico do Problema 3.108 forem aumentados lentamente, determine a a intensidade T dos maiores torques que podem ser aplicados ao eixo e b o comprimento da parte C D que pe