Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas fundamentais - Ex. 02
A roda de 300 kg tem um raio de giração em relação a seu centro de massa O de . Se a roda é submetida a um momento de binário , determine sua velocidade angular 6 s após ela partir do repouso e sem deslizar. Também determine a força de atrito que se desenvolve entre a roda e o solo.
Passo 1
Começaremos o exercício aplicando o princípio do impulso e da quantidade de movimento com relação ao ponto O para descobrir a velocidade angular final da roda:
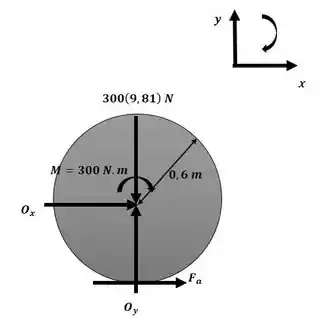
Passo 2
Agora iremos aplicar o princípio do impulso e da quantidade de movimento linear na direção x para descobrir o valor da força de atrito:
Resposta
Exercícios de Livros Relacionados
A bola sólida de massa m é solta com uma velocidade v 1 sobre a aresta do degrau áspero. Se ela repica horizontalmente no degrau com uma velocidade v 2 , determine o ângulo no qual o contato ocorre. S
A bobina de 50 kg é submetida a uma força horizontal P = 150 N. Se a bobina rola sem deslizar, determine sua velocidade angular 3 s após ela partir do repouso. O raio de giração da bobina em relação a
As engrenagens A e B de massa 10 kg e 50 kg têm raios de giração em relação a seus centros de massa respectivos k A = 80m m e k B = 150m m . Se a engrenagem A é submetida ao momento de binário M = 10N
A roda de 60 kg tem um raio de giração em relação a seu centro O de k O = 300m m . Se ela é submetida a um momento de binário M = 3 t 2N . m , onde t é dado em segundos, determine a velocidade angular