Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 56

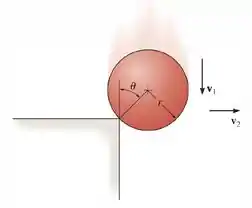
A bola sólida de massa m é solta com uma velocidade v 1 sobre a aresta do degrau áspero. Se ela repica horizontalmente no degrau com uma velocidade v 2 , determine o ângulo no qual o contato ocorre. Suponha que não há deslizamento quando a bola bate no degrau. O coeficiente de restituição é e .

Passo 1

Uma vez que o peso da bola sólida é uma força não-impulsiva, o momento angular é conservado em torno da ponta do degrau. O momento de inércia da bola em torno de seu centro de massa é

I O = 2 5 m r 2

Passo 2

Através do esquema abaixo, podemos obter ω 2 ,   r ' e r ' ' .

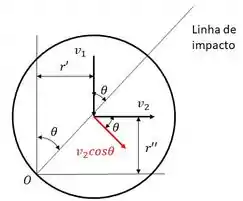
Logo,

ω 2 = v 2 c o s θ r

r ' = r s e n θ

r ' ' = r c o s θ

Como o momento angular do sistema em torno da ponta do degrau é conservado, temos:

( H O ) 1 = ( H O ) 2

[ m v b ) 1 r ' = I O ω 2 + [ m b v b ) 2 r ' '

Logo,

( m v 1 ) ( r s e n θ ) = 2 5 m r 2 v 2 c o s θ r + ( m v 2 ) ( r c o s θ )

v 2 v 1 = 5 7 t a n θ           ( 1 )

Passo 3

Em virtude da choque entre a bola e o degrau deve-se aplicar a equação do coeficiente de restituição. Assim, temos:

e = 0 - ( v b ) 2 ( v b ) 1 - 0

e = - v 2 s e n θ - v 1 c o s θ

v 2 v 1 = e c o s θ s e n θ             ( 2 )

Substituindo (1) em (2), obtemos:

5 7 t a n θ = e c o s θ s e n θ

tan 2 ⁡ θ = 7 5 e

θ = tan - 1 ⁡ 7 5 e

Resposta

O ângulo no qual ocorre o contato entre a bola e o degrau é igual a tan - 1 ⁡ 7 5 e .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ventilador sopra o ar a 162m 3 / m i n . Se o ventilador pesa 150N( m ≈ 15k g ) e tem um centro de gravidade em G , determine o menor diâmetro d de sua base, necessário para que ele não tombe. O pes
O borrifador de brinquedo para crianças consiste de uma coberta de 0,2k g e uma mangueira que tem massa por comprimento de 30g / m . Determine a vazão da água através do tubo de 5m m de diâmetro, de m
A curva está conectada ao cano nos flanges em A e B como mostra a figura. Se o diâmetro de cano é 0,3m e ele transmite uma descarga de 1,35m 3 / s , determine as componentes horizontal e vertical da r
O cotovelo de um cano subterrâneo de 125m m de diâmetro é submetido a uma pressão estática de 80k N / m 2 . A velocidade da água que passa por dentro dele é v = 2,4m / s . Supondo que as conexões do c
A cúpula hemisférica de massa m é mantida em equilíbrio pelo jato vertical de água descarregado por um bocal de diâmetro d . Se a descarga de água através do bocal é Q , determine a altura h a que a c