Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas fundamentais - Ex. 05
A bobina de 50 kg é submetida a uma força horizontal P = 150 N. Se a bobina rola sem deslizar, determine sua velocidade angular 3 s após ela partir do repouso. O raio de giração da bobina em relação a seu centro de massa é .
Passo 1
Começaremos o exercício calculando o momento de inércia da bobina em relação a seu centro de massa:
Passo 2
Agora iremos aplicar o princípio do impulso e quantidade de movimento linear na direção x com o auxílio da imagem a seguir:
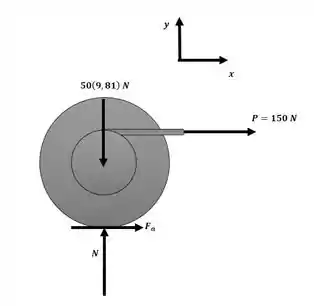
Essa será nossa equação 1.
Passo 3
Agora iremos aplicar o princípio do impulso e da quantidade de movimento angular para o sistema ainda com o auxílio do esquema apresentado no passo 2:
Agora, substituindo a equação 1 nessa expressão:
Resposta
Exercícios de Livros Relacionados
O escoadouro é usado para desviar o curso da água, Q = 0,6m 3 / s . Se a água tem uma área de seção transversal de 0,05m 2 , determine as componentes da força, no pino D e no rolete C , necessárias pa
Uma lancha é propelida pelo motor a jato mostrado na figura. A água do mar é puxada pela bomba, a uma vazão de 0,54m 3 / s , através de uma entrada A , de 150m m de diâmetro. Uma hélice acelera a vazã
O pêndulo consiste de uma esfera de 5k g e uma barra de 2k g . Se ele é solto do repouso quando θ = 90 ° , determine o ãngulo θ de repique após a esfera bater no chão. Considere e = 0,8 .
O centro de massa da bola de 1,5k g tem uma velocidade v G 1 = 1,8m / s quando ela acerta a extremidade da barra fina lisa de 2,5k g que está em repouso. Determine a velocidade angular da barra em tor
A barra A B de 2 kg está pendurada na posição vertical. Um bloco de 1 k g , deslizando sobre uma superfície horizontal lisa com uma velocidade de 3,6m / s , acerta a barra na sua extremidade B. Determ