Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas fundamentais - Ex. 04

As engrenagens A e B de massa 10 kg e 50 kg têm raios de giração em relação a seus centros de massa respectivos k A = 80   m m e k B = 150   m m . Se a engrenagem A é submetida ao momento de binário M = 10   N . m , determine a velocidade angular da engrenagem B 5 s após ela partir do repouso.

Passo 1

Começaremos o exercício calculando os momentos de inércia das engrenagens A e B:

I A = m k A 2 = 10 0,08 2 → I A = 0,064   k g   . m 2

I B = m k B 2 = 5 0 0,15 2 → I A = 1,125   k g   . m 2

E agora encontraremos a relação entre as velocidades angulares das engrenagens:

ω A = r B r A ω B = 0,2 0,1 ω B

ω A = 2 ω B

Passo 2

Agora iremos aplicar o princípio do impulso e quantidade de movimento angular para a engrenagem A com o auxílio do esquema a seguir:

↺ +   I A ω A 1 + ∑ ∫ t 1 t 2 M A d t = I A ω A 2

0 + 10 ( 5 ) - ∫ 0 5 s F 0,1 d t = 0,064 [ 2 ω B 2 ]

∫ 0 5 s F d t = 500 - 1,28 ω B 2

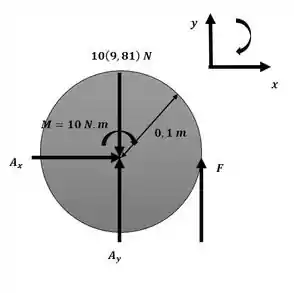
Essa será nossa equação 1.

Passo 3

Agora iremos aplicar o princípio do impulso e da quantidade de movimento angular para a engrenagem B com o auxílio do esquema a seguir:

↺ +   I B ω B 1 + ∑ ∫ t 1 t 2 M B d t = I B ω B 2

0 + ∫ 0 5 s F 0,2 d t = 1,125 ω B 2

∫ 0 5 s F d t = 5,625 ω B 2

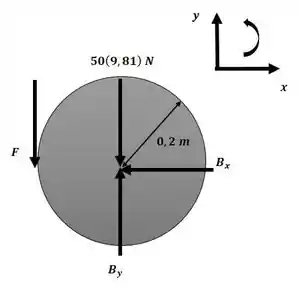
Agora iremos igualar essa expressão à nossa equação 1 para obter o valor da velocidade angular no instante final:

500 - 1,28 ω B 2 = 5,625 ω B 2

ω B 2 = 72,4   r a d / s

Resposta

ω B 2 = 72,4   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a barra OA de massa desprezível é submetida ao momento de binário M = 9 N.m, determine a velocidade angular da engrenagem interior de 10 kg para t = 5 s após ela partir do repouso. A engrenagem tem
O carretel tem um peso de 750 N e um raio de giração em relação a seu centro de gravidade k G = 0,375m . Se ele é submetido a um torque M = 37,5 N.m e parte do repouso quando o torque é aplicado, dete
Mostre que, se uma placa está girando em torno de um eixo fixo perpendicular à placa e passando pelo seu centro de massa G, a quantidade de movimento angular é a mesma quando calculada em relação a qu
Em um dado instante, o corpo tem uma quantidade de movimento linar L = m v G e uma quantidade de movimento angular H G = I G ω calculados em relação a seu centro de massa. Mostre que a quantidade de m
Se a corda é submetida a uma força horizontal P = 150 N, e a cremalheira está fixa ao plano horizontal, determine a velocidade angular da engrenagem em 4 s, partindo do repouso. A massa da engrenagem