Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 93
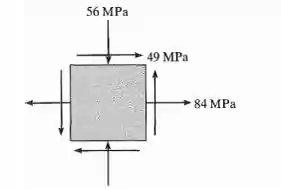
O elemento está sujeito às tensões mostradas na Figura. Se σe = 350 MPa, determine o fator de segurança para essa carga com base na (a) teoria da tensão de cisalhamento máxima e (b) teoria da energia de distorção máxima.
Passo 1
Fala galera, vamos primeiro para a letra a
- Primeiramente, vamos analisar as tensões dadas pelo problema. Sabemos que:
O próximo passo é determinar as tensões principais, para que peguemos o caso mais crítico. Sabemos que as tensões principais são dadas por:
Substituindo, teremos:
Usando a teoria da tensão de cisalhamento máxima:
Substituindo e isolando o fator de segurança, teremos:
Passo 2
A letra b nos pede para utilizar a energia de distorção máxima, que será dada por:
Substituindo e isolando o fator de segurança, teremos:
Resposta
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A chapa é feita de bronze Tobin, que escoa a σ e = 175M P a . Pela teoria de falha da tensão de cisalhamento máxima, determine a tensão de tração máxima σ x que pode ser aplicada à chapa, se também fo
A tensão de escoamento para uma liga de magnésio e zircônio é σ e = 107M P a . Se uma peça de máquina for fabricada com esse material e um ponto crítico no material for submetido às tensões principais
Um material está sujeito ao estado plano de tensão. Expresse a teoria da falha da tensão de cisalhamento máxima em termos de σ x , σ y , τ x y . Considere que as tensões principais têm sinais algébric
Resolva o Problema 10.67 usando a teoria de energia de distorção máxima
As componentes do estado plano de tensão em um ponto crítico de uma carcaça de aço estrutural A - 36 são mostradas na figura. Determine se ocorreu falha (escoamento) com base na teoria da energia de d