Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 42

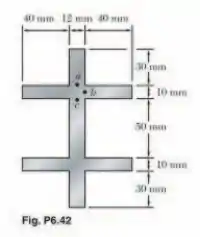
Sabendo que uma dada força cortante vertical V causa uma tensão de cisaIhamento máxima de 50 MPa em um elemento de paredes finas com a seção transversal mostrada, determine a tensão de cisalhamento correspondente no (a) ponto a, (b) ponto b, (c) ponto c.

Passo 1

E aí gurizada, tudo certinho? O enunciado pede que a gente determine a tensão de cisalhamento correspondentes aos pontos a, b, e c localizados na figura anterior. Vamos descobrir?

Q a = ( 12 ) ( 30 ) ( 25   10   15 ) = 18   x   10 ³ m m ³

Q b = ( 40 ) ( 10 ) ( 25   + 5 )   = 12 x 10 ³ m m

Passo 2

Considerando os dados abaixo:

                                            t a = t c = t m = 12 m m

t b = 10 m m

t m = 50 M P a

Partiu determinar a tensão de cisalhamento ;)

                                      a     t a t m = Q a Q m . t m t a = 18 49.35 . 12 12 = 0,36474 x 50   M P a = 18,23   M P a

b     t b t m = Q b Q m . t m t b = 12 49.35 . 12 10 = 0,29179 x 50   M P a = 14,59   M P a

c     t c t m = Q c Q m . t m t c = 45.6 49.35 . 12 12 = 0,92401 x   50 M P a = 46,2   M P a

Resposta

t a = 18,23   M P a

t b = 14,59   M P a

t c = 46,2   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos D e E : (b) a maior tensão de cisalhamento,
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos D e E : (a) a maior tensão normal.
146. A viga caixão é mostrada é feita de quatro pranchas firmemente coladas. Sabendo-se que na junta colada a tensão admissível de cisalhamento é de 830k P a , determinar: (a) a maior força cortante v
147. Para a viga caixão do problema 5.146 , determinar (a) a maior força cortante horizontal permissível na viga; (b) a correspondente tensão de cisalhamento máximo na viga
148. Duas forças são aplicadas a um tubo A B , como mostrado. Sabendo-se que o tubo tem diâmetros, interno e externo, iguais a 35m m e 42m m , respectivamente, determinar as tensões, normal e de cisal