Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas Revisão - Ex. 147

147. Para a viga caixão do problema 5.146 , determinar (a) a maior força cortante horizontal permissível na viga; (b) a correspondente tensão de cisalhamento máximo na viga

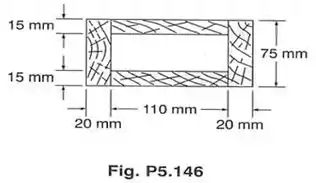
Passo 1

E aí meus queridos! Aqui vamos nós de novo, continuar nossa saga em Resistência dos Materiais

E a missão dessa vez, é basicamente a mesma coisa do exercício anterior

A única diferença é que dessa vez, queremos a maior força cortante horizontal e a corresponde tensão máxima de cisalhamento na viga.

Desse modo, já vou adiantando que os eixos que usaremos pra resolver essa questão, vão ser diferentes da anterior.

Se liga só! Para resolvermos esse problema, precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita.

Então, bora seguir em frente! A nossa fórmula para o cisalhamento, mencionada acima, é dada por...

τ = Q V I t

Isolemos o V ...

V = τ I t Q

Por essa relação, sabemos que...

τ = t e n s ã o   c i s a l h a n t e

V = e s f o r ç o   c o r t a n t e

Q = m o m e n t o   e s t á t i c o

I = m o m e n t o   d e   i n é r c i a

t = e s p e s s u r a   d o   p o n t o   q u e   c a l c u l a m o s   o   c i s a l h a n t e

Agora que já sabemos o que cada termo da fórmula significa, vamos identificar cada um desses valores na nossa seção.

Passo 2

Para isso, precisamos determinar primeiramente a linha neutra na nossa seção. A linha neutra de uma seção retangular uniforme oca sempre fica no centro da nossa seção.

a) Como o que queremos inicialmente, é saber a força cortante máxima que devemos aplicar, considerando a junta entre as tábuas; então bora redesenhar nossa viga...

Uma vez que a força cortante é horizontal, para resolver essa questão nós vamos mudar de eixo. Deixando a figura fixa, se antes a linha neutra passava por ela horizontalmente, agora a linha neutra passa verticalmente.

Se sentir dúvida, saiba que é comum representar a linha neutra como perpendicular a direção da força cortante. Uma força cortante horizontal implica uma linha neutra vertical!

Captou! Se sim; repara na nossa bela imagem a seguir...

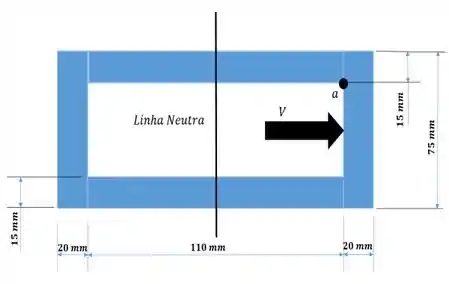
Que belezinha, né não!? E como pode ver, linha neutra na vertical e força cortante na horizontal.

Pois muito bem! Vamos começar calculando o momento de inércia da nossa seção transversal. Ele é dado pela diferença entre o momento de inércia do retângulo cheio menos o momento de inércia do retângulo vazio.

Se tá ruim de entender, talvez a imagem abaixo ajude...

As coisas aqui vão ser um pouco diferentes do exercício anterior. Como nossa linha neutra está na vertical, o que era base ou comprimento (como queira chamar) lá vira altura aqui...

Sendo assim... Pela figura, identificamos que o retângulo vazio tem as seguintes dimensões abaixo...

A l t u r a   h 2 = 110   m m

C o m p r i m e n t o   b 2 = 75   m m - 2 ⋅ 15   m m = 45   m m

Já o retângulo cheio...

A l t u r a   h 1 = 150   m m

C o m p r i m e n t o   b 1 = 75   m m

Desse modo, nosso momento de inércia será igual à...

I = 1 12 b 1 h 1 3 - 1 12 b 2 h 2 3

I = 1 12 ( 75 ) ( 150   m m ) 3 - 1 12 ( 45   m m ) ( 110   m m ) 3

I = 16102500   m m 3 = 1,61025 ⋅ 10 - 5   m ³

Passo 3

Voltando nossa atenções de novo pra primeira imagem do P a s s o   2 ; nela podemos ver um ponto preto que chamamos de a . Ele está na junta de ligação entre as tábuas.

Esse ponto será fundamental para obtermos o esforço cortante máximo na junta...

Pra ficar mais legal ainda... Bora fazer um esboço considerando só da reta delimitada pelo ponto a pro lado direito. Fazendo isso, obtemos a região destacada de vermelho abaixo com a linha que passa pelo seu centro de massa já à mostra...

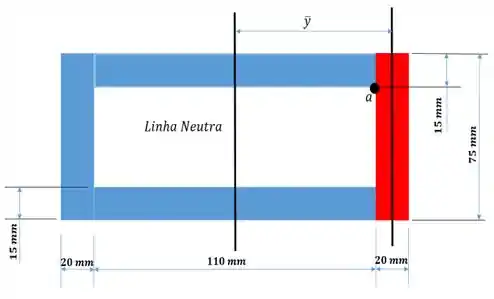
Onde para o ponto a , temos a seguinte espessura...

t = 20   m m + 20   m m

t = 40   m m = 0,04   m

Isso aí garotinho(a)! Estamos indo bem!

Veja bem! O centro de massa do retângulo vermelho está a uma distância y - da nossa linha neutra, igual a:

y - = 55   m m + 20   m m 2

y - = 65   c m

Logo, fica fácil obter o nosso momento estático! Ele é dado pelo produto da área do retângulo vermelho pela distância y - ...

Q = A y -

Q = 75   m m 20   m m ( 65   m m )

Q = 97500   m m 3 = 9,75 ⋅ 10 - 5   m 3

E então, o nosso esforço cortante máximo, (pegando a fórmula do P a s s o   1 ) será igual a...

V = τ I t Q

V = 830   k P a ( 1,61025 ⋅ 10 - 5   m ³ ) ( 0,04   m ) 1,61025 ⋅ 10 - 5   m ³

V = 33200   N

Bora guardar ele, hein!? Vamos precisar pra letra (b)

Passo 4

b) No segundo item, o objetivo é encontrar a correspondente tensão de cisalhamento máximo na viga.

Ora bolas! O ponto onde há maior cisalhamento na nossa peça é o ponto sobre a linha neutra. Sendo assim, sobre a linha neutra, bora nomear um ponto b .

De modo que, assim como na letra (a), é preciso fazer um esboço considerando só da parte da linha neutra pro lado direito.

E obtemos então, a seguinte imagem abaixo...

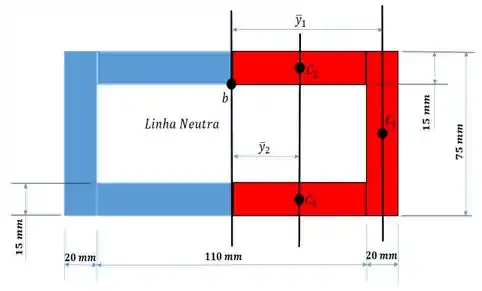
Fazendo o mesmo procedimento da letra (a), e tomando dessa vez o ponto b como nosso ponto de análise, a nossa espessura t correspondente é de...

t = 15   m m + 15   m m

t = 30   m m

O momento de inércia por sua vez, continua o mesmo e igual à...

I = 1,61025 ⋅ 10 - 5   m ³

Já em relação ao momento estático Q , as coisas vão ser um pouco diferentes... Uma vez que nossa área aumentou, hein!?

Além daquele retângulo anterior, temos dois outros retângulos para incluir em nossos cálculos, como demonstrado na figura abaixo, destacados com os numerais 1 , 2 e 3 .

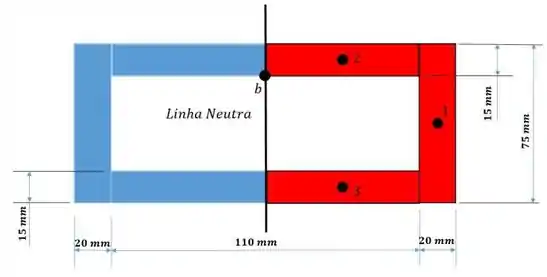
Os retângulos 2 e 3 tem a mesma área, viu!? Só pra constar!

A 2 = A 3

Assim, levando em consideração essas duas últimas figuras, o nosso momento estático será dado pela seguinte fórmula abaixo...

Q = A 1 y - 1 + 2 A 2 y - 2

E substituindo os valores numéricos podemos obter o quanto vale Q ...

Q = A 1 y - 1 + 2 A 2 y - 2

Q = 75   m m 20   m m ( 65   m m ) + 2 55   m m 15   m m ( 27,5   m m )

Q = 142875   m m 3 = 1,42875 ⋅ 10 - 4   m 3

Feito isso! Basta pegar a fórmula da tensão cisalhante e trocar as variáveis pelos valores obtidos. Só lembrando que o V aqui, é o que descobrimos anteriormente, hein!?

τ m á x = Q V I t

τ m á x = ( 1,42875 ⋅ 10 - 4   m 3 ) ( 33200   N ) ( 1,61025 ⋅ 10 - 5   m ³ ) ( 0,03   m )

τ m á x = 9819282,72   P a ≅ 9,82   M P a

E pronto! Finalizamos aqui!

Até a próxima!

Rumo a aprovação!

Resposta

a) V = 33200   N

b) τ m á x ≅ 9,82   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois perfis laminados de aço W 130 × 23.8 podem ser soldados em A e B , de qualquer uma das três maneiras mostradas, para formar uma viga composta. Sabendo-se que para cada uma das soldas a força cisa
Uma placa de 4 mm de espessura é encurvada como mostrado e depois usada como uma viga. Para uma força cortante vertical de 12 kN, determinar (a) a tensão de cisalhamento no ponto A; (b) a máxima tensã
Determinar a tensão cisalhamento no ponto A de um tubo na parede fina como a seção transversal mostrada, casada por uma força cortante vertical V.
O projeto de uma viga requer a soldagem de quatro placas horizontais à uma placa vertical de 12,7x127 mm como mostrado. Para uma força cortante vertical V determinar a dimensão h para que o fluxo de c
Uma viga extrudada tem seção transversal como mostrado e uma espessura uniforme da parede de 4 mm. Para uma força cortante vertical de 12 kN, determinar a tensão de cisalhamento nos quatro pontos indi