Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 37
Sabendo que , determine a resultante das três forças indicadas.
Passo 1
Pessoal esse problema fala sobre um assunto muito importante que é a decomposição das forças!!
Ué, mas não é para achar a resultante? É sim! Mas faremos isso decompondo todas as forças nos eixos e que facilita a soma!
Olha só como funciona!
Passo 2
Bom galera, a gente vai encontrar as componentes horizontais e verticais de cada uma das forças que é dada por:
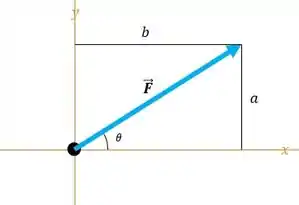
Aqui a força é a força que queremos decompor e as forças e são as decomposições nos eixos e , respectivamente.
Ta vendo que as forças formam um triângulo retângulo? Então, é com base nesse triângulo retângulo que a gente tem as seguintes equações:
Agora vamos ver as decomposições:
Passo 3
Show de bola, a gente vai calcular a resultante calculando separadamente a resultante no eixo e no eixo :
Calculando cada força:
Perceba que os ângulos vão se somando!! No caso de o ângulo foi tão grande que inverteu o sentido da força e ela acabou negativa!
E agora o eixo :
Agora é só somar:
Passo 4
Se lembra da primeira equação que a gente achou? Era essa aqui:
Como a gente só achou as componentes vertical e horizontal da força, ainda não chegamos no resultado já que o problema pede a intensidade da força resultante, assim vamos utilizar essa equação da forma: