Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 140

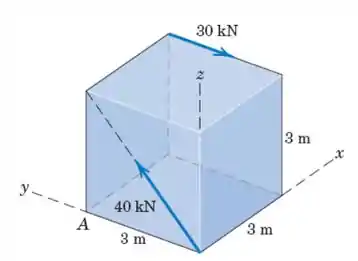
Substitua as duas forças que atuam no cubo de 3   m por uma única força equivalente   F   e m   A  e um binário  M .

Passo 1

E aí meus queridos, tudo bom com vocês?Vamos pra mais um problema, mas relaxem que esse é bem tranquilo. Desejamos uma força que substitua as duas que estão na imagem por uma única, no entanto, essa força deve gerar o mesmo momento que da situação original. Pois bem, antes de tudo vamos achar essa força resultante que vai substituir as duas forças apresentadas. Começando pela componente x teremos

R x = 0

Pois não temos nenhuma componente das forças na direção x . Observando agora o eixo y teremos

R y = - 30 + 40 ⋅ cos ⁡ 45 ° ≈ - 1,716   j ^

De maneira análoga para o eixo z temos

R z = 40 ⋅ s en ⁡ 45 ° ≈ 28,3   k ^

Sendo assim, nossa força resultante que pode substituir os dois vetores é

R = R x + R y = - 1,716   j ^ + 28,3   k ^

Passo 2

Calma, dá uma respirada que nosso problema tá quase finalizado. Falta só encontramos o momento inicial que vai ser o mesmo gerado pela nossa força resultante. Lembrando que a direção do momento é dada pela regra da mão direita vamos ter

M a = 3 ⋅ 30   k ^ - 40 ⋅ s e n 45 ° ⋅ 3   i ^   k N ⋅ m

M a = 90   k ^ - 84,85   i ^   k N ⋅ m

Pronto, tá resolvido nosso problema.

Resposta

R = - 1,716   j ^ + 28,3   k ^

M a = 90   k ^ - 84,85   i ^   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os dois elementos estruturais, um sob tração e o outro sob compressão, exercem as forças indicadas no nó O . Determine o módulo da resultante R das duas forças e o ângulo θ que R faz com o eixo x posi
Um cabo esticado entre os suportes fixos A e B está sob uma tração T de 900N . Usando os vetores unitários i e j expresse a tração como um vetor; primeiramente como uma força T A atuando em A e, em se
Determine o módulo F s da força trativa atuando na mola, para que a resultante de F s e de F seja uma força vertical. Determine o módulo R dessa força resultante vertical.
Para o mecanismo do Prob. 2/9, determine os componentes escalares P t e P n de P , que são tangente e normal, respectivamente, à manivela B C .
Determine a resultante R das duas forças mostradas(a) aplicando a regra do paralelogramo para a adição vetorial e(b) somando as componentes escalares.