Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 20
Sabendo que a força nos parafusos é proporcional ao momento de primeira ordem da região em verde e a força aplicada no parafuso A é 280N. Determine a força aplicada no parafuso B.
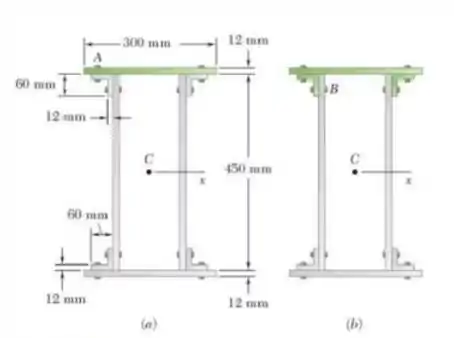
Passo 1
Fala aí galera, vamos pra mais um problema de estática. Primeiramente, vamos determinar o momento de primeira ordem em A:
Agora, vamos calcular o momento de primeira ordem em B. Primeiro, precisamos determinar o centroide da peça. Passando um plano de referência na base da área verde, teremos:
Precisamos somar com a distância do plano de referência até o centroide da peça, logo:
Logo, o momento de primeira ordem em B será:
Passo 2
Agora, para determinar a força, vamos fazer uma regra de 3:
Resposta
Exercícios de Livros Relacionados
Determine as coordenadas do centro de massa do suporte, que é construído a partir de uma chapa de espessura uniforme.
O tanque de armazenamento de água é uma concha de revolução e deve ser pulverizado com duas camadas de tinta que tem uma cobertura de 500 pés2 por galão. O engenheiro (que se lembra da mecânica) consu
Determine a massa do comprimento de um quarto de círculo da mangueira do radiador. O diâmetro interno é 40 mm, a espessura da parede é 4 mm e a densidade do material de borracha é 1050 kg / m3.
A área de um quarto circular é girada 360 ° em torno do eixo y. Determine o volume do corpo resultante, que é uma parte de uma esfera.
O corpo mostrado em seção transversal é um anel circular completo formado pela rotação da área octogonal em torno do eixo z. Toda a superfície deve ser coberta com um revestimento especial. Determine