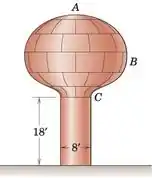
O tanque de armazenamento de água é uma concha de revolução e deve ser pulverizado com duas camadas de tinta que tem uma cobertura de 500 pés2 por galão. O engenheiro (que se lembra da mecânica) consulta um desenho em escala do tanque e determina que a linha curva ABC tem um comprimento de 34 pés e que seu centroide está a 8,2 pés da linha central do tanque. Quantos galões de tinta serão usados para o tanque incluindo a coluna cilíndrica vertical?

Quanto ao cilindro, precisamos encontrar a distância do centro de massa ao eixo vertical. Como o corte bidimensional de um cilindro em relação ao eixo z é um círculo, a distância do eixo vertical ao centro do círculo é , então, neste caso:

E o perímetro das laterais do cilindro é:

Em seguida, precisamos encontrar , uma vez que a revolução é 360, escrevemos:

Finalmente, estamos procurando encontrar a Área da superfície aqui, então usaremos a primeira fórmula do Teorema de Pappus:

Usando isso para ambos os corpos, uma vez que a superfície total é a soma dos corpos individuais:

Como sabemos que sabemos que nossa tinta pode cobrir 500 pés2 por galão de tinta, dividimos a área com 500 para ver quanta tinta precisamos para uma cobertura

Como queremos descobrir quanta tinta é necessária para duas capas, multiplicamos o número acima por 2