Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 74
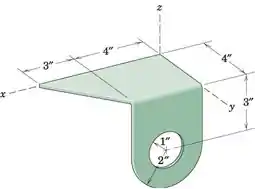
Determine as coordenadas do centro de massa do suporte, que é construído a partir de uma chapa de espessura uniforme.
Passo 1
Lembre-se da teoria de que as coordenadas do centroide de um objeto podem ser encontradas usando a (s) equação (ões):
No entanto, no caso de densidade constante e um objeto bidimensional, podemos escrever a massa como:
A partir daqui, as equações se tornam
Fazendo isso para todas as equações
Passo 2
Tenha muito cuidado com a localização do eixo. Eu não posso enfatizar isso o suficiente. Lembre-se de que tudo o que fazemos e o resultado será em relação a esse eixo. Tenha isso em mente e esses problemas se tornam muito mais simples
Aqui, separamos o problema em 5 partes, conforme mostrado na figura. Começaremos com a parte 1. Usando o Problema Resolvido 5/2 e o fato de que o ponto onde as duas alturas do triângulo se encontram é 4 unidades na direção X positiva, podemos encontrar a massa e o centro de massa. (No caso de você estar confuso, ignoramos densidade e espessura porque são constantes para todos os corpos, então se cancelam, o que significa que encontramos apenas Área.). Observe que Z = O é um plano de simetria.
Passo 3
Em seguida, temos uma folha de metal retangular. Os planos de simetria são Z = 0, X = 2, Y = 2 e, uma vez que estamos ignorando a densidade e a espessura, a massa será a Área:
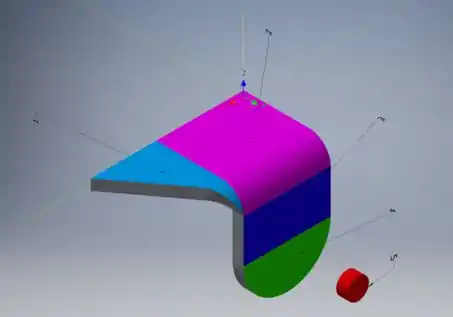
O terceiro corpo é semelhante ao segundo. Planos de simetria são X = 2, Y = 4 e z = 3, então:
Passo 4
O quarto corpo é uma folha semicírculo, então sua massa seria a metade de uma folha circular completa. O centro de massa está relacionado ao centro do círculo e essa relação pode ser encontrada no Problema Resolvido 5/3. O centro do círculo tem coordenadas (2,3, -3) e este corpo tem planos de simetria X = 2, Y = 4 então:
Finalmente, temos um buraco circular. Por ser um buraco, ele terá massa negativa. O centro de massa de uma folha circular cai sobre o centro do círculo e como este corpo compartilha um ponto central com o corpo 4 e os mesmos planos de simetria, escrevemos:
Passo 5
Encontramos todas as informações de que precisamos para resolver esse problema, então, usando as fórmulas que obtemos:
Resposta
Separe os corpos em cinco e consulte o Problema Resolvido 5/3 para obter as coordenadas individuais dos centros de massa de cada corpo. Lembre-se também de usar planos de simetria onde quer que possam ser usados. Por fim e muito importante nunca se esqueça de onde está o nosso eixo de referência e onde está o Problema de amostra, então faça os ajustes necessários! As unidades dos resultados estão em polegadas e das áreas ao quadrado em polegadas!