Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 22
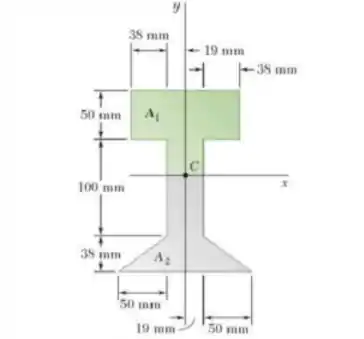
Calcule o momento de primeira ordem de cada componente de superfície em relação a x e explique os resultados:
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o momento de primeira ordem. Sabemos que ele é a distância do centroide da área acima do ponto e o centroide da área total multiplicado pela área acima do ponto, logo:
Logo, o momento estático será:
Resposta
Exercícios de Livros Relacionados
Derive expressões para o cortante V e o momento M em termos de x para a viga em balanço de Prob. 5/114 mostrado novamente aqui. O carregamento é parabólico.
Um pedreiro estica uma corda entre dois pontos separados por 50 pés no mesmo nível com uma tensão de 10 libras em cada extremidade. Se a corda pesa 0,1 lb, determine a flexão h no meio da corda.
Localize o centroide x - , y - da área da seção transversal.
Localize o centroide do elemento.
Localize o centroide do elemento.