Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 86

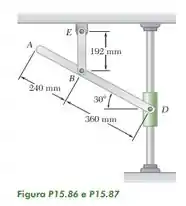
Sabendo que no instante mostrado na figura a velocidade angular da barra BE é de 4   r a d   / s no sentido anti-horário, determine (a) a velocidade angular da barra AD, (b) a velocidade do colar D, (c) a velocidade do ponto A.

Passo 1

Questão 86 agora, meus chapas!

Bom! Pra começar, vamos fazer um esboço da porta, representando vetorialmente as velocidades que estão agindo em A , B e D e o centro de rotação instantâneo.

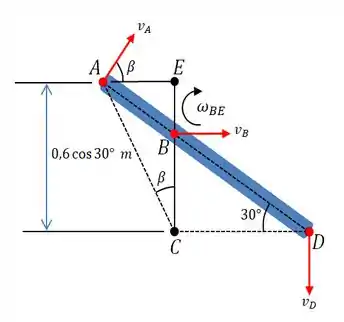
Passo 2

a) Primeiro, temos que determinar a velocidade angular da barra A D .

Vamos começar, analisando a barra E B ! Temos que...

v B = r B / E ω B E = E B ω B E

Como ω B E = 4   r a d / s , no sentido anti-horário, então...

v B = ( 4   r a d / s ) ( 0,192   m )

v B = 0,768   m / s   →

A gente tem aí, que o centro de rotação passa por C .

Temos então, que a mesma velocidade v B que encontramos anteriormente, pode ser escrita como...

v B = r B / C ⋅ ω A D = B C ω A D

Isolando a velocidade angular da barra A D ...

ω A D = v B B C

ω A D = 0,768   m / s 0,360 sin ⁡ 30 °   m

ω A D = 4,27   r a d / s   ⤸

Obtemos o valor de ω A D ... Que está no sentido horário, pois v B aponta para a direita, fazendo com que a barra A D gire nesse sentido!

Passo 3

b) Em seguida, bora correr atrás da velocidade do colar, v D !

A gente tem que...

v D = r D / C ω = D C ω

v D = 0,360 cos ⁡ 30 °   m ( 4,27   r a d / s )

v D = 1,331   m / s   ↓

Passo 4

c) Pra obter v A , aí vai dar um pouco mais de trabalho! Mas nada que a gente aqui não tire de letra!

Precisamos do comprimento A C , que é o nosso r A / C !

Bom! A gente tem que...

A E = 0,240 cos ⁡ 30 °   m = 0,20875   m

C E = 0,600 sen ⁡ 30 °   m = 0,3000   m

E o ângulo β é dado por...

β = tan - 1 ⁡ 0,20875 0,3000 = 34,7 °

Logo, podemos descobrir A C , usando Pitágoras...

( A C ) 2 = A E 2 + C E 2

( A C ) 2 = 0,20875   m 2 + 0,3000   m 2

A C = 0,20875   m 2 + 0,3000   m 2

A C = 0,36497   m

E então, v A , será dada por...

v A = A C ω A D

v A = 0,36497   m ( 4,27   r a d / s )

v A = 1,558   m / s

Escrevendo na forma de módulo e ângulo...

v A = 1,558   m / s   ∠ 34,7 °

Pronto! Terminamos aqui!

Hasta la vista, guys!

Resposta

a)

ω A D = 4,27   r a d / s   ⤸

b)

v D = 1,331   m / s   ↓

c)

v A = 1,558   m / s   ∠ 34,7 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

25. O motor gira a engrenagem A de maneira que sua velocidade angular aumenta uniformemente de zero para 3000 rev/min após o eixo girar 200 revolucoes. Determine a velocidade angular da engrenagem D q
6. O mecanismo acima para acionar a janela de um carro é mostrado na figura. Aqui a maçaneta faz girar a pequena engrenagem C, que gira a engrenagem de dentes retos S, dessa maneira girando a alavanca
11. O abridor de latas opera de tal maneira que a lata é acionada pela roda motriz D, Se o eixo do induzido S no motor gira com uma velocidade angular constante de 40 rad/s, determine a velocidade ang
10. Durante uma rajada de vento, as pás do moinho de vento são submetidas a uma aceleração angular a = 0,2 θr a d / s 2 , onde θ é dado em radianos. Se inicialmente as pás têm uma velocidade angular d
5. A operação da engrenagem de marcha à ré em uma transmissão automotiva é mostrada. Se o motor gira o eixo A em ω A = 40 r a d s , determine a velocidade angular do eixo de transmissão, ω B . O raio