Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 85
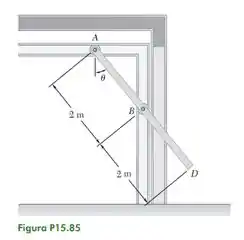
Uma porta basculante é guiada por roletes em A e B que rolam em uma pista horizontal e uma vertical. Sabendo que, quando , a velocidade do rolete B é de para cima, determine (a) a velocidade angular da porta, (b) a velocidade da extremidade D da porta.
Passo 1
Questão 85 agora, meus chapas!
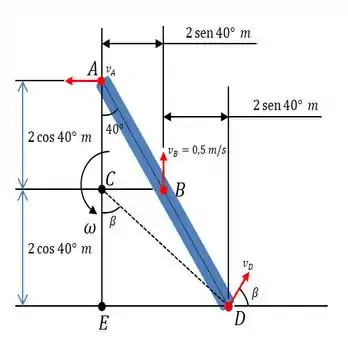
Bom! Pra começar, vamos fazer um esboço da porta, representando vetorialmente as velocidades que estão agindo em , e .
Passo 2
a) A gente tem aí, que o centro de rotação instantâneo passa por .
E como o enunciado nos diz que a velocidade do rolete é de para cima, ou seja, , então podemos usar a seguinte relação...
No sentido anti-horário, né!? Já que tende a fazer a porta girar nesse sentido!
Passo 3
b) Em seguida, bora correr atrás do !
Para isso, primeiro precisamos ir atrás daquele ângulo ali do enunciado.
De boinhas! É só usar a relação arco-tangente...
Obtido , vamos atrás de , que é distância entre e o eixo por onde passa o centro de rotação instantâneo...
E então, será dada por...
Escrevendo em módulo e ângulo...
Resposta
a)
b)