Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 121

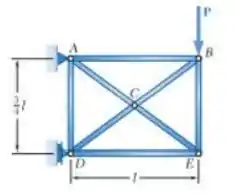
Sabendo que as oito barras da treliça indeterminada mostradas nas figuras têm a mesma área de seção transversal, determine o esforço na barra .

Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Primeiro, vamos substituir a barra na extremidade e substituímos a força da barra pela carga atuando na barra na extremidade :

A parte constante sai do somatório, logo:

Logo, a deflexão em vai ser:

Sabendo disso, vamos utilizar as equações de equilíbrio para encontrar as forças nos braços da treliça. No nó , temos:

E também:

Já no nó , teremos:

E também:

Já no nó , temos:

Passo 2

E então, vamos preencher a tabela abaixo a fim de calcularmos os somatórios para a deflexão. Fica assim:

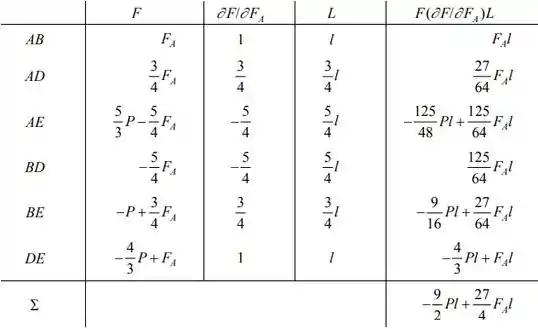
Assim, a deflexão vai ser dada pela pela relação que a gente achou lá no início. Substituindo:

Isolando a força em , temos:

Portanto, o esforço na barra vai ser:

É isso, galera Bora pra próxima?

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra composta do Problema 2.104, se P cresce gradualmente desde zero até a deflexão do ponto C atingindo um valor máximo σ m e depois retorna a zero, pede-se determinar o máximo valor de P, a

Uma barra de 300 mm de comprimento e seção transversal retangular de 20 × 50m m consiste em duas lâminas de aço doce, cada uma com 6m m de espessura coladas a uma lâmina central de 8 mm de espessura,

Para a barra composta do Problema 2.106, de P cresce gradualmente desde zero até 375k N e depois retorna a zero, pede-se determinar a máxima deformação na barra, a máxima tensão em cada lâmica e, a de

Uma barra de 300 mm de comprimento e seção transversal retangular de 20 × 50m m consiste em duas lâminas de aço doce, cada uma com 6m m de espessura coladas a uma lâmina central de 8 mm de espessura,

A temperatura da barra composta do P r o b .2.43 é aumentada para 80 ° C . Sabendo-se que, para o aço E = 200G P aeα = 11,7.10 - 6° C - 1 , para o latão E = 105G P aeα = 20,9.10 - 6° C - 1 , e que nen