Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 131

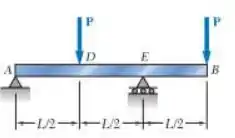
Para a viga prismática mostrada, determine a inclinação no ponto D .

Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Primeiro, vamos determinar as reações nos apoios:

∑ M E = 0 - A L + P L 2 - P L 2 + M 0 = 0 A = M 0 L

E também:

∑ M A = 0 E L - P L + L 2 - P L 2 + M 0 = 0 E = 2 P - M 0 L

Passo 2

Em seguida, sabemos que a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação. Portanto:

U = U A D + U D E + U E B

E então, a inclinação no ponto C vai ser:

θ D = ∂ U ∂ M 0 = ∂ U A D ∂ M 0 + ∂ U D E ∂ M 0 + ∂ U E B ∂ M 0

Então, temos que calculara inclinão para cada porção da viga. Para a porção A D , dada no intervalo 0 ≤ x ≤ L 2 , temos:

U A D = ∫ 0 L / 2   M 2 2 E I d x

Dado que o momento fletor nesta porção vai ser:

M = M 0 L x

Logo:

∂ M M 0 = x L M = 0

Substituindo, vamos encontrar a deformação para esta porção:

∂ U A D ∂ M 0 = 1 E I ∫ 0 L / 2   M ∂ M M 0   d x = 0 ∂ U A D ∂ M 0 = 0

Vamos repetir o processo para a porção D E . Temos:

U D E = ∫ L / 2 L   M 2 2 E I d x

E para o momento, temos:

M = A x - P x - L 2 - M 0

Assim:

∂ M M 0 = x L - 1 M = - P x - L 2

Portanto, a inclinação nesta porção vai ser:

U D E = 1 E I ∫ L / 2 L   M ∂ M M 0   d x

Substituindo:

∂ U D E ∂ M 0 = P L 3 48 E I

Por último, para a porção E B , temos:

U E B = ∫ 0 L / 2   M 2 2 E I d x

Dado que:

M = - P v ∂ M ∂ M 0 = 0

Substituindo:

∂ U E B ∂ M 0 = 1 E I ∫ 0 L 2 M ∂ M M 0   d v = 0 ∂ U E B ∂ M 0 = 0

Portanto, a inclinação no ponto D vai ser:

θ D = ∂ U A D ∂ M 0 + ∂ U D E ∂ M 0 + ∂ U E B ∂ M 0 θ D = P L 2 48 E I

É isso, galera Bora pra próxima?

Resposta

θ D = P L 2 48 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das barras mostradas é feita de um aço com tensão de escoamento igual a σ e = 250M P a e o módulo de elasticidade de E = 200G P a . Sabendo-se que l = 380m m , determinar a máxima energia de
Resolver o Prob. 10.10, quando a = 1,8 m .
Uma força P de intensidade 10k N é aplicada em cada uma das barras de aço mostrada. Usando E = 200G P a , determinar:a energia de deformação absorvida pela barra a ;o comprimento necessário l , se a e
A barra A B é feita de uma liga de alumínio para a qual a tensão de escoamento é σ e = 300M P a e o módulo de elasticidade é E = 75G P a ; a barra B C é feita de um tipo de aço para o qual a σ e = 420
A barra A B é feita de um aço de alta resistência para o qual σ e = 750M P a e E = 200G P a . Uma energia de deformação de 25J deve ser acumulada pela barra quando a força axial P é aplicada. Sabendo-