Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 104

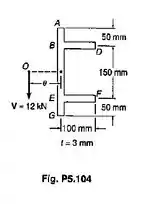
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.

Passo 1

Fala aí galera, bora pra mais uma questão de Resmat. O primeiro passo é determinar os momentos de inércia das partes da estrutura:

I B D = I E F = 100 × 3 3 12 = 225 m m 4

I A G = 3 × 2 5 0 3 12 = 3906250 m m 4

Logo, o momento de inércia total será:

I = ∑ I = 3906700 m m 4

Passo 2

Agora, vamos pegar parte por parte para fazermos nossa análise. Para a parte BD, temos que:

Q = 1,5 × 10 0 × 3 = 450 m m ³

Logo:

τ = V Q I t = 12000 × 450 3 × 225 = 8000 M P a

Logo:

F 1 = τ A = 8000 × 3 × 100 = 2400000 N

Passo 3

Agora, faremos o mesmo para AG:

Q = 100 × 3 × 50 = 15000 m m ³

Logo:

τ = V Q I t = 12 000 × 15000 3 × 3906250 = 15,36 M P a

Logo:

F 2 = τ A = 250 × 3 × 15,36 = 11520 N

Passo 4

Portanto, o centro de cisalhamento será dado por:

∑ M = V e

Logo:

12 000 e = 75 × 2400000 + 1,5 × 11520

e = 15001,44 m m

Resposta

e = 15001,44 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a localização e do centro de cisalhamento (ponto O) para o tubo que tem uma fenda ao longo de seu comprimento
Determine a localização e do centro de cisalhamento (ponto O) para o elemento de paredes finas que tem a seção transversal mostrada na figura.
A força P é aplicada à alma da viga como mostra a figura. Se e = 250 m m , determine a altura h da aba direita de modo que a viga sofra deflexão para baixo sem torção. Os segmentos do elemento têm a m
A viga é composta por quatro tábuas pregadas como ostra a figura. Determine a força de cisalhamento à qual cada prego ao longo dos lados C e da parte superior D deve resistir se estiverem uniformement
Se a viga T for submetida a um cisalhamento vertical V=60kN, determine a tensão de cisalhamento máxima na viga. Calcule também o salto da tensão de cisalhamento na junção aba-alma AB. Trave um rascunh