Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas Revisão - Ex. 188
Resolva o problema 7.187, se cada uma das cargas de for aplicada separadamente na viga.
Passo 1
Fala aí galera do Responde aí, bora pra outra questão. Essa questão é muito parecida com a anterior, mas temos que fazer por partes.
Primeiramente, precisamos fazer os diagramas de cortante e momento. Para isso, precisamos calcular as reações. Primeiro, vamos considerar apenas a carga da esquerda.
Sabemos que o somatório de momentos em uma rótula deve ser nulo tanto pela esquerda como pela direita, logo:
Além disso, o somatório de forças na vertical e horizontal deve ser nulo. Primeiramente, irei considerar a força em D para baixo. Logo:
Note que temos 2 equações que relacionam e logo, fazendo um sistema:
Passo 2
Agora, basta fazer os diagramas pedidos:
Diagrama de cortante:
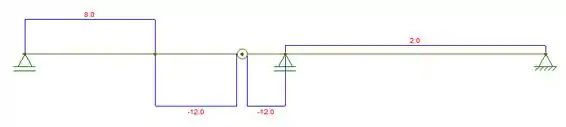
Diagrama de momento:
Passo 3
O próximo passo é determinar a seção da estrutura, sabendo as tensões admissíveis. As tensões são dadas por:
Portanto, devemos pegar o máximo momento e o máximo cortante nos diagramas e substituir para achar as maiores tensões na estrutura e fazer com que elas sejam iguais às tensões admissíveis. Com isso isolamos o para dimensionar a seção. Ou seja:
Agora, vamos analisar qual valor escolher. Note que, o momento de inércia da seção é diretamente proporcional a e que a tensão é inversamente proporcional ao momento de inércia. Logo, para a menor tensão, devemos escolher o maior Ou seja:
Passo 4
Agora, vamos fazer o mesmo, mas considerar apenas a carga da direita.
Sabemos que o somatório de momentos em uma rótula deve ser nulo tanto pela esquerda como pela direita, logo:
Além disso, o somatório de forças na vertical e horizontal deve ser nulo. Logo:
Note que temos 2 equações que relacionam e logo, fazendo um sistema:
Passo 5
Agora, basta fazer os diagramas pedidos:
Diagrama de cortante:
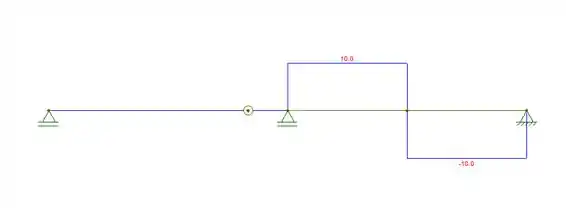
Diagrama de momento:
Passo 6
O próximo passo é determinar a seção da estrutura, sabendo as tensões admissíveis. As tensões são dadas por:
Portanto, devemos pegar o máximo momento e o máximo cortante nos diagramas e substituir para achar as maiores tensões na estrutura e fazer com que elas sejam iguais às tensões admissíveis. Com isso isolamos o para dimensionar a seção. Ou seja:
Agora, vamos analisar qual valor escolher. Note que, o momento de inércia da seção é diretamente proporcional a e que a tensão é inversamente proporcional ao momento de inércia. Logo, para a menor tensão, devemos escolher o maior Ou seja:
Resposta
Agora, basta fazer os diagramas pedidos:
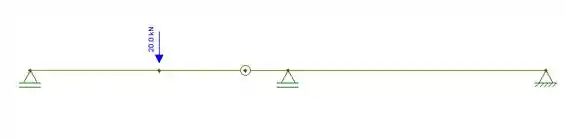
Diagrama de cortante:
Diagrama de momento:
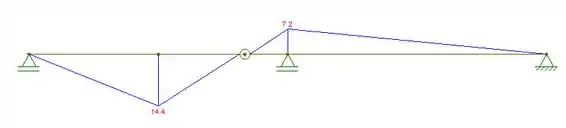
Agora, basta fazer os diagramas pedidos:
Diagrama de cortante:
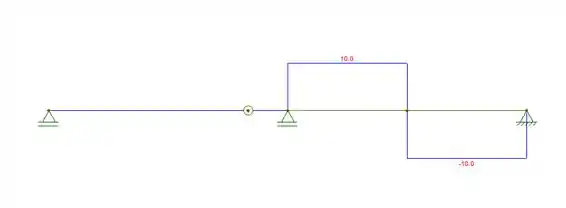
Diagrama de momento:
