Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 22
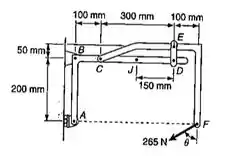
Sabendo-se que a haste de ligação DE tem 25,4mm de largura e 3,2mm de espessura, determine a tensão normal na porção central desta haste quando .
Passo 1
Vamos desenhar o diagrama de corpo livre da barra CEF, com ele conseguiremos a reação no pino DE, que nos interessa. As forças foram arbitradas da maneira abaixo:
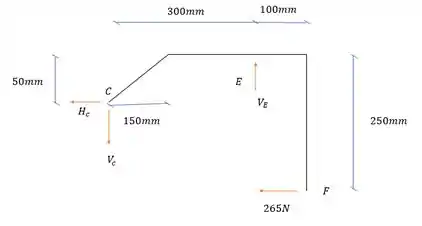
Vamos fazer o somatório dos momentos no ponto C, e encontrar a reação em E. Sentido anti-horário positivo.
Passo 2
Agora transferimos o esforço para a barra DE, que desce invertido fazendo a barra se comprimir. Calculamos a área da barra e logo a tensão normal.
Resposta
Exercícios de Livros Relacionados
Determine a menor área admissível para a seção transversal da barra D E da treliça mostrada, se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar 138M P a .
Para a treliça e carregamento mostrado, determine a tensão normal na barra B D . Sabendo-se que a área da seção transversal da barra é de 1 . 290m m ² ².
Determine a menor área admissível para a seção transversal da barra D E da treliça mostrada se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar 200M P a .
Para a treliça e carregamento mostrado, determine a tensão normal na barra A D . Sabe-se que a área da seção transversal da barra é de 1.200m m ² ².
Duas barras cilíndricas, uma de aço ( E = 200G P a ) e outra de latão ( E = 105G P a ), são ligadas em C e engastadas em A e E . Para o carregamento indicado, determinar: (a) as reações em A e E ; (b)