Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 17
Para a treliça e carregamento mostrado, determine a tensão normal na barra . Sabendo-se que a área da seção transversal da barra é de .
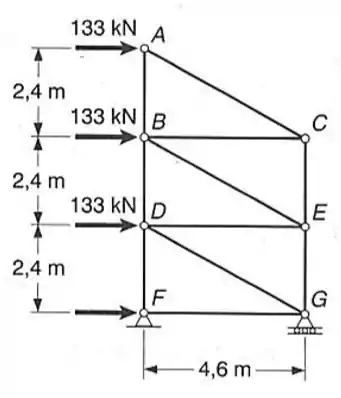
Passo 1
O problema já deu a área de seção transversal e pede a tensão normal, logo basta calcular a força a qual a barra está submetida. Para isso podemos utilizar o método dos nós ou das seções ou ambos. Neste caso ambos serão utilizados.
Passo 2
Primeiro vamos analisar o nó , utilizando o método dos nós. Para ambos os métdos vamos sempre considerar que as forças são de tração! Caso sejam de compressão vamos ver que o resultado será negativo.
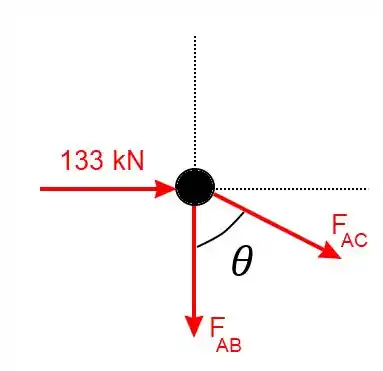
é o ângulo da figura.
A partir daí vamos tirar as duas equações de equilíbrio referentes ao eixo e ao eixo :
Passo 3
Agora que temos a força em , vamos utilizar o método das seções para descobrir a força na barra .
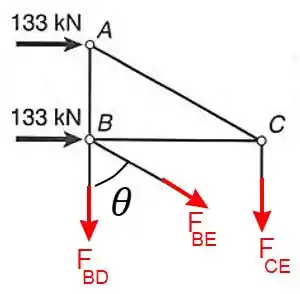
Para achar a força atuante em basta utilizarmos a componente horizontal
Passo 4
Agora podemos analisar o nó :
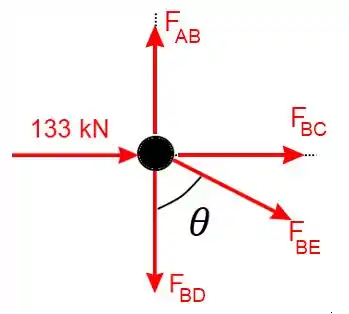
Como queremos não precisamos nos preocupar com as forças na horizontal então:
Passo 5
Agora basta aplicar a equação da tensão normal: