Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 18
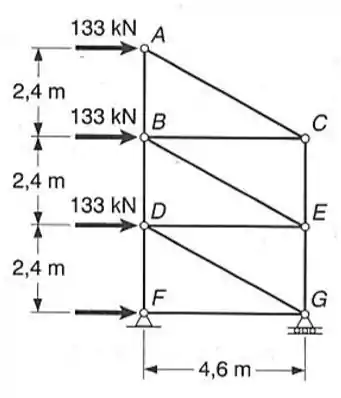
Determine a menor área admissível para a seção transversal da barra da treliça mostrada, se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar .
Passo 1
O problema já deu a tensão normal e pediu a área, logo basta calcular a força a qual a barra está submetida. Para isso podemos utilizar o método dos nós ou das seções ou ambos.
Passo 2
Vamos utilizar o método das seções para descobrir a força na barra .
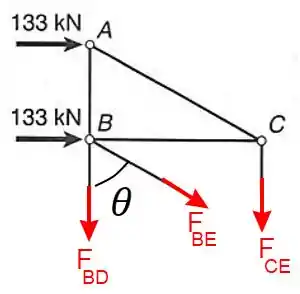
Para achar a força atuante em basta utilizarmos a componente horizontal
Passo 3
Vamos olhar agora o nó
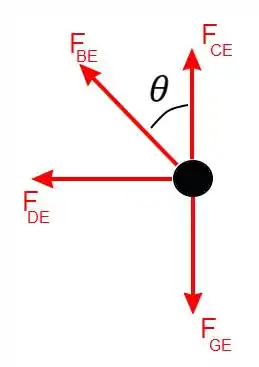
Aqui o ângulo () é o mesmo de antes, pela geometria da figura (são alternos internos).
Como queremos então nós só precisamos olhar para as forças na horizontal, logo:
Passo 4
Aplicando a fórmula da tensão normal.
Resposta
Exercícios de Livros Relacionados
Para a barra composta do Prob. 2.9, determinar ( a ) a carga, para a qual a deformação total da barra resulta nula; ( b ) a correspondente deflexão no ponto B .
Uma carga vertical P é aplicada em A, na seção superior de um tronco de cone de altura h , raio mínimo a e raio máximo b . (a) Determine a deflexão no ponto A, se E for o módulo de elasticidade.
Duas barras cilíndricas maciças são ligadas em B e carregadas como mostrado. A barra A B é de aço ( E = 200G P a ) e a barra B C é de latão ( E = 105G P a ) . Determinar: ( a ) a deformação total da b
Duas barras cilíndricas maciças são ligadas em B e carregadas como mostrado. A barra A B é de aço ( E = 200G P a ) e a barra B C é de latão ( E = 105G P a ) . Determinar: ( a ) a deformação total da b
Uma coluna de concreto de 1,2 m de altura é reforçada por quatro barras de aço, cada uma com 20 m m de diâmetro. Sabendo-se que os módulos de elasticidade para o concreto e aço são 25 M P a e 200 M P