Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 2
Sabendo-se que a mola torcional em B em A é de constante k e que a barra AB é rígida, determinar a carga crítica PCR
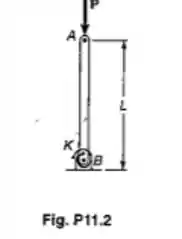
Passo 1
Fala aeee galera, bora resolver mais um exercício de flambagem? Bom, vamos começar desenhando o nosso diagrama de corpo livre:
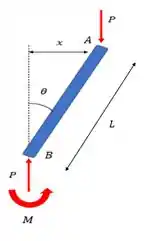
A nossa meta é encontrar o nosso peso crítico, relacionando P com M e .
Analisando a figura a gente tem que:
E o momento da mola torcional é dado por:
Passo 2
Vamos fazer o somatório dos momentos no ponto B, pra gente enfim relacionar o nosso
Com o momento de reação da mola, considerando o sentido horário positivo:
E substituindo os valores:
E aqui vem o bizu! Como a gente tá trabalhando com pequenos ângulos a gente pode usar:
E aí:
E esse é o nosso peso crítico:
Resposta
Exercícios de Livros Relacionados
Uma carga axial P é aplicada a uma barra de aço AB de diâmetro 35 mm, como mostrado. Quando P= 90 KN observa-se na barra uma deflexão horizontal de 0,75 mm no seu ponto médio C. Usando E= 200 GPa dete
Uma coluna AB suporta uma seção transversal uniforme e é contraventada no plano xz em seu ponto médio C. Pede-se: a) determinar a relação b/d para que o coeficiente de segurança em relação a flambagem
W 360 × 216 , com as propriedades geométricas mostradas. Utilizando um fator de segurança igual a 2,6, determine a carga central admissível se o comprimento efetivo da coluna é de 6,5m. Utilize E = 20
Determine a carga crítica de uma tábua de madeira com 3ft de comprimento e seção transversal retangular de 3 16 × l 1 4 i n . articulado nas suas extremidades. Utilize E = 1,6 × 1 0 6 p s i .
Uma coluna de comprimento de flambagem L pode ser feita colando-se pranchas idênticas em um dos arranjos mostrados na figura. Determine a relação entre as forças críticas usando o arranjo a e o arranj