Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 11

Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (a) a maior tensão normal; (b) a tensão de cisalhamento no ponto a ; (c) a maior tensão de cisalhamento.

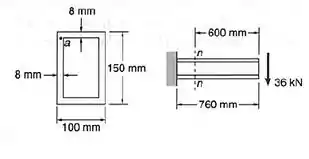
Passo 1

Para calcular o que ele pede nas alternativas, vamos precisar do momento de inércia da seção. Vamos calcular ele logo então.

Por simetria, vemos que o centroide fica bem no meio da seção, onde a gente vai chamar de y - = 0 .

Precisamos calcular o momento de inércia em relação a esse eixo. Usando o Teorema dos Eixos paralelos e lembrando que para um retângulo de base b e altura h , o momento é:

I R = b h 3 12

Separamos a seção em quatro retângulos e calculamos:

I = ∑ I + A d 2

I = 2 0,1 ⋅ 0,008 3 12 + 0,1 ⋅ 0,008 ⋅ 0,0 71 2 + 2 0 , 008 ⋅ 0,0 134 3 12

I = 4,04454 ⋅ 10 - 6   m 4

Passo 2

(a) Queremos a maior tensão normal na seção n - n . Essa tensão vai ser causada pelo momento na seção, que vale:

M = 36 ⋅ 10 3 ⋅ 0,6 = 21600   N ⋅ m

E vai estar localizada no ponto na seção mais distante do eixo y - = 0   (linha neutra), que vale:

c = 0,15 2 = 0,075   m

Agora é só a gente usar a fórmulinha de tensão normal devido a flexão:

σ = M c I = 21600 ⋅ 0,075 4,04454 ⋅ 10 - 6

σ = 400,5   M P a

Passo 3

(b) Para achar a tensão de cisalhamento no ponto a , vamos usar a fórmulinha:

τ m é d = V Q I t

Vamos considerar a área do retângulo que fica acima do eixo horizontal que passa por a . Ela vale:

A = 0,008 ⋅ 0,1 = 0,0008   m 2

A distância entre o centroide dessa área e o da seção é y - 1 = 0,071   m . Então:

Q = A y - 1 = 0 , 0008 ⋅ 0,071 = 5,68 ⋅ 10 - 5   m 3

Como t é a expressura da seção no eixo que passa por a :

t = 2 ⋅ 0,008 = 0,016   m

E já que o esforço cortante na seção é V = 36 ⋅ 10 3 N :

τ m é d a = 36 ⋅ 10 3 ⋅ 5,68 ⋅ 10 - 5 4,04454 ⋅ 10 - 6 ⋅ 0,016 = 31,6   M P a

Passo 4

(c) A maior tensão de cisalhamento acontece na linha neutra, em y - = 0 . Precisamos descobrir o centroide da área A da seção acima desse eixo.

Dividindo essa área em 3 retângulos:

y - 2 = ∑ y i - A i ∑ A i = 0,071 0,1 ⋅ 0,008 + 2 ⋅ 0,0335 ⋅ 0,067 ⋅ 0,008 0,1 ⋅ 0,008 + 2 0,067 ⋅ 0,008

y - 2 = 0,04952   m

Nossa Q fica assim:

Q = A y - 2 = 0,1 ⋅ 0,008 + 2 0,067 ⋅ 0,008 ⋅ 0,04952

Q = 9,27 ⋅ 10 - 5   m 3

O t continua 0,016   m e V = 36 ⋅ 10 3 N , então:

τ m á x = V Q I t = 36 ⋅ 10 3 ⋅ 9,27 ⋅ 10 - 5 4,04454 ⋅ 10 - 6 ⋅ 0,016

τ m á x = 51,6   M P a

Resposta

(a) σ = 400,5   M P a

(b) τ m é d a = 31,6   M P a

(c) τ m á x = 51,6   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é feita de um material cerâmico cuja tensão de flexão admissível é σ a d m = 5 MPa e tensão de cisalhamento τ a d m = 2,8 MPa. Determine a largura b da viga, se a altura for h=2b.
A viga T de aço em balanço foi montada com duas chapas soldadas como mostra a figura. Determine as cargas máximas P que podem ser suportadas com segurança pela viga, se a tensão de flexão admissível f
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se cada prego puder suportar uma força de cisalhamento de
A viga é construída com duas tábuas presas uma à outra na parte superior e na parte inferior por duas fileiras de pregos espaçados de 150 mm. Se uma força de cisalhamento interna V = 3 k N for aplicad
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250m m e o cisalhamento apl