Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 149

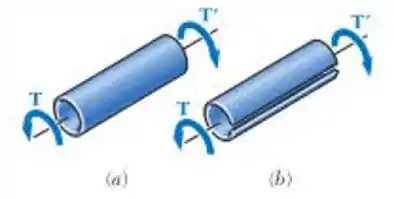
São aplicados torques iguais a tubos com paredes finas de mesmo comprimento Lm, mesma espessura t e mesmo raio c . Um dos tubos foi cortado no sentido do comprimento, como mostra a figura. Determine (a) a relação τ b / τ a das tensões de cisalhamento máximas nos tubos e (b) a relação ∅ b / ∅ a dos ângulos de torções dos eixos.

Passo 1

E ai galerinha tudo beleza? O enunciado pede que a gente determine a relação τ b / τ a das tensões de cisalhamento máximas nos tubos e a relação ∅ b / ∅ a dos ângulos de torções dos eixos. Para isso vamos começar pela parte do elemento sem fenda :D

Sem fenda:

Área delimitada na linha central. a = π c 2 τ a = T 2 t a = T 2 π c 2 t J ≈ 2 π c ³ t       φ a = T L G J = T L / 2 π c ³ t G

Com fenda: a = 2 π c ,     b = t ,       a b = 2 π c t ≫ 1 c 1 = c 2 = 1 3 τ b = T c 1 a b 2 = 3 T 2 π c t 2 φ b = T c 2 a b 3 G = 3 T L 2 π c t 3 G

Passo 2

Agora podemos determinar as relações de tensões e de torque respectivamente 0/

  1. Relação de tensão :

    2. τ b τ a = 3 T L 2 π c t ²   x 2 π c 2 t T = 3 c t

  2. Relação de torção:

φ b φ a = 3 T L 2 π c t ³ G   x 2 π c t 3 G T L = 3 c 2 t 2

Resposta

  1. τ b τ a = 3 c t
  2. φ b φ a = 3 c 2 t 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No problema 7,124 , determine a máxima tensão nromal e a máxima tensão cisalhante no ponto L .
O tanque de ar comprimido A B tem um diâmetro externo de 250m m e espessura de parede de 8m m . Ele é equipado com um anel no qual é aplicada uma força P de 40k N horizontal em B . Sabendo que a press
Um anel de latão com diâmetro externo de 127m m e espessura de 6,35m m se encaixa exatamente dentro de um anel de aço com diâmetro interno de 127m m e 318m m de espessura, quando a temperatura de ambo
O tanque mostrado tem um diâmetro interno de 180m m e uma espessura de parede de 12m m . Sabendo que ele contém ar comprimido sob pressão de 8M P a , determine a intensidade T do torque aplicado para
Um reservatório de gás esférico feito de aço tem um diâmetro externo de 6096 mm e parede com espessura de 11,1 mm. Sabendo que a pressão interna é de 517,1 kPa, determine a tensão normal máxima e a te