Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 52

A seção transversal de uma viga extrudada é um quadrado vazado de lado a = 3   i n . e espessura t = 0,25 . Para uma força cortante vertical de 15   k i p s ,determine a tensão de cisalhamento máxima na viga e esquematize o fluxo de cisalhamento na seção transversal.

Passo 1

Então gurizada, vamos realizar mais esse cálculo? Comecemos pelo esboço a seguir :D

I u = I v = 1 12 ( 3,25 4 - 2,75 4 ) = 4,53125   i n 4

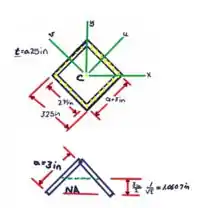
Produtos da Inércia: I x = I y = I u = I v I x = 4,53125   i n 4

V = 15   k i p s

Q N A = 2 3   i n × 0,25   i n ( 1,0607   i n ) = 1,59105   i n 3

τ m = π N A = V Q N A I ( 2 t ) = ( 15   k i p s ) ( 1,59105   i n 3 ) ( 4,53125   i n 4 ) ( 2 ) ( 0,25   i n ) = 10,53   k s i

Resposta

10,53   k s i .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força cortante vertical é de 1200 lb em uma viga com a seção transversal mostrada na figura. Sabendo que d = 4 pol., Determine a tensão de cisalhamento no (a) ponto a, (b) ponto b..
Sabendo que uma dada força cortante vertical V causa uma tensão de cisaIhamento máxima de 50 MPa em um elemento de paredes finas com a seção transversal mostrada, determine a tensão de cisalhamento co
O cisalhamento vertical é de 1200 lb em uma viga com a seção transversal mostrando. Determine (a) a distância d para a qual a  b, (b) o tensão de cisalhamento correspondente nos pontos a e b.
A viga de alumínio extrudada tem espessura de parede constante de in. Sabendo que a força cortante vertical na viga é de 2 kips, determine a tensão de cisalhamento correspondente em cada um dos cinco
Quatro cantoneiras de aço 1,202 x 102 x 9,5 e uma placa de 12 x 400 mm são parafusadas de modo a formar a viga de seção transversal mostrada. Os parafusos tem diâmetro de 22mm e são espaçados longitud