Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas de Revisão - Ex. 72

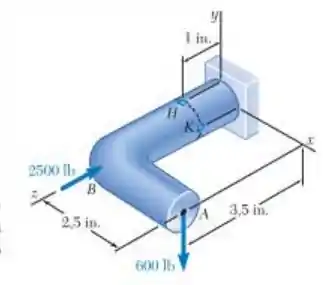
Forças são aplicadas nos pontos A e B do suporte em ferro fundido mostrado. Sabendo que o suporte tem um diâmetro de 0,8in., determine as tensões principais e a máxima tensão de cisalhamento no (a) ponto H, (b) ponto K.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine as tensões principais e a máxima tensão de cisalhamento no (a) ponto H, (b) ponto K. Considere meu lindo esboço

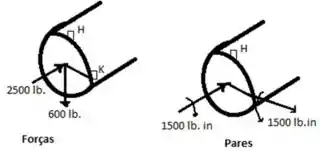
Passo 2

Então gurizada na seção contentando pontos H e K,

P = 2500 l b c o m p r e s s i o n

V y = - 600 l b

V x = 0

M x = 3,5 - 1 600 = 1500 l b ∙ i n .

M y = 0

M z = - 2,5 600 = - 1500 l b ∙ i n .

c = 1 2 d = 0,4 i n .

A = π c 2 = 0,50265 i n 2

Agora podemos determinar a inércia :D

I = π 4 c 4 = 20,106 × 10 - 3 i n 4

J = 2 I = 40,212 × 10 - 3 i n 4

Para um semicírculo

Q = 2 3 c 3 = 42,667 x 10 - 3 i n 3

Passo 3

  1. No ponto H temos:

    2. σ H = P A + M c I = - 2500 0,50265 + 1500 0,4 20,106 × 10 - 3 = 24,87 × 10 3 p s i

    τ H = T c J = 1500 0,4 40,212 × 10 - 3 = 14,92 × 10 3 p s i

    σ a v e = 24,87 2 = 12,435 k s i

    R = 24,87 2 2 + 14,92 2 = 19,423 k s i

    σ m a x   = σ a v e + R σ m a x   = 31,9 k s i

    σ m i n = σ a v e - R     σ m i n   = - 6,99 k s i

    τ m a x = 1 2 σ m a x - σ m i n τ m a x = 19,42 k s i

    Passo 4

  2. No ponto K,

σ K = P A = - 2500 0,50265 = - 4,974 × 10 3 p s i

τ K = T c J + V Q I t = 1500 0,4 40,212 × 10 - 3 + 600 42,667 × 10 - 3 20,106 × 10 - 3 0,8  

= 16,512 × 10 - 3 p s i

σ a v e = - 4,974 2 = - 2,487 k s i

R = - 4,974 2 2 + 16,512 2 = 16,698 k s i

σ m a x = σ a v e + R   σ m a x = 14,21 k s i

σ m i n   = σ a v e - R   σ m i n = - 19,18 k s i

τ m a x   = 1 2 σ m a x - σ m i n   τ m a x   = 16,70 k s i

Resposta

  1. σ m a x   = 31,9 k s ,     σ m i n   = - 6,99 k s i   e     τ m a x = 19,42 k s i
  2. σ m a x = 14,21 k s i σ m i n = - 19,18 k s i   e   τ m a x   = 16,70 k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três placas de aço, cada uma com 13mm de espessura, são soldadas para formar uma viga em balanço. Para o carregamento mostrada, determine as tensões normal e de cisalhamento nos pontos a e b
8.57 Quatro forças são aplicadas a um perfil de aço laminado W8x28, conforme mostra a figura. Determine as tensões principais e a tensão de cisalhamento máxima no ponto a.
8.59 Uma força P é aplicada a uma viga em balanço por meio de um cabo preso a um parafuso localizado no centro da extremidade livre da viga. Sabendo que P atua em uma direção perpendicular ao eixo lon
a
β = 0) e com seu eixo longitudinal AB horizontal, determine a intensidade da força P para a qual a tensão normal no ponto a é +120Mpa, (b) Resolva a parte a considerando que a viga é instalado com β =