Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 118
Uma suspensão de eixo duplo para uso em caminhões pequenos é mostrada na figura. A massa da estrutura central F é de 40 kg, e a massa de cada roda e elo conectado é de 35 kg com centro de massa de 680 mm da linha central vertical. Para uma carga L = 12kN transmitida à estrutura F, calcule a força de cisalhamento total suportada pelo pino em A.
Passo 1
Primeiro, vamos desmembrar o dispositivo e desenhar a roda direita e o link anexado
Peso da roda é
Observe que a força de reação BX é igual a zero, o que pode ser mostrado igualando a soma das forças na direção x a zero
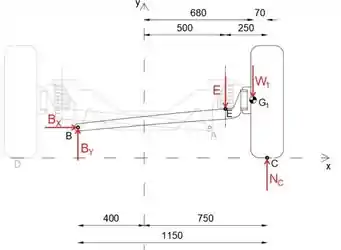
Ao igualar a soma das forças momentos sobre o ponto C a zero, eliminaremos a força de reação normal do solo, portanto, podemos escrever a conexão entre as forças BY e a força na mola E
Passo 2
Como a estrutura do carro e o carregamento são simétricos, podemos escrever a conexão entre a força de reação AY e a força na mola F
(2)
Sabemos que a força de reação AY e BY são iguais
(3)
Portanto, podemos escrever a expressão (1) como
(4)
Passo 3
O próximo passo é desmembrar o dispositivo e desenhar o diagrama de corpo livre da moldura central
O peso do quadro central é
Passo 4
Agora vamos igualar a soma das forças na direção y a zero
E, substituindo F, BY e E pelas expressões (2), (3) e (4), obteremos a equação em que AY é o único desconhecido
Uma vez que a força de reação em A tem apenas componente vertical, sua magnitude é igual a ela