Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 113
Se o segmento da comporta for grande o suficiente, a comporta estará prestes a abrir. Determinar o comprimento desse segmento para que isso ocorra. A comporta é articulada em e tem uma largura de . A densidade da água é .
Passo 1
O problema pede que encontremos o comprimento de para que a comporta fique a ponto de abrir.
Bom galera, então a gente já vai começar calculando a intensidade da carga da água nas profundidades do ponto e , então vamos lá:
Agora na profundidade de :
Passo 2
Beleza, agora a gente vai tentar simplicar fazendo um diagrama das comportas recebendo essas cargas:
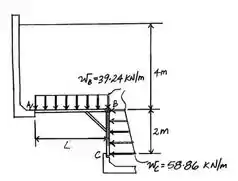
Assim, as forças aplicadas pela água em cada comporta fica:
Passo 3
Show de bola, pra gente ver se a comporta vai abrir a gente tem que calcular o momento usando como eixo de rotação o ponto , vamos lá:
Lembrando que a carga da água tem um centro próprio, que fica no centroide da força.